Ciągłość funkcji
jakubs: Zbadaj ciągłość funkcji:
| | sinx | |
f(x)= |
| x≠0 i f(0)=1 |
| | |x| | |
Pasuję policzyć granicę w punkcie 0(prawostronną i lewostronną), ale nie wiem jak

10 sie 16:29
Ajtek:
| | sinx | |
Dla x>0 f(x)= |
| , liczysz pochodną licznika i mianownika  |
| | x | |
| | sinx | |
Dla x<0 f(x)= |
| i to samo  . |
| | −x | |
Jeśli się mylę to poprawcie mnie.
10 sie 16:42
Mila:
Granicę lewostronną i prawostronną.
Jeśli limx→0f(x) =f(0) to funkcja jest ciągła.
10 sie 16:49
jakubs: Tyle, że ja pochodnych nie znam, a zadanie jest ze zbiorku Krysickiego również przed
pochodnymi, jest jakiś sposób na obliczenie tego bez pochodnych ?
10 sie 16:49
zombi: | | sinx | |
A znasz granicę |
| → 1, gdy x→0? |
| | x | |
10 sie 17:00
jakubs: Tak, ale jak wyznaczyć tę granicę, to nie wiem. Na wykładzie od PWr była tylko informacja o
tym, ale bez rozwiązania, mam to przyjąć że tak jest. Tutaj jest jeszcze wartość bezwzględna i
nie mam żadnego pomysłu jak to obliczyć

10 sie 17:05
zombi:
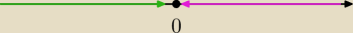
x→0
−, x "idą" od lewej w stronę zera, więc są ujemne tak? Natomiast x→0
+, czyli x "idą od
prawej strony do zera, więc są dodatnie, prawda?
Zielone: x→0
−
Fioletowe: x→0
+
Skoro wiesz jakie będą przyjmowały wartości (ujemne/dodatnie) te nasze iksy, wiesz już jak
opuszczać moduł z mianownika, czy ze znakiem + czy ze znakiem −
10 sie 17:39
jakubs: | | sinx | |
limx→0+ |
| czyli to będzie dążyć do 1 |
| | x | |
| | sinx | |
limx→0− |
| a to do −1 |
| | −x | |
Tak ?
10 sie 19:42
Dzidka:
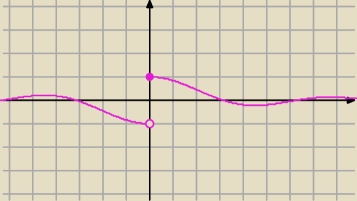
Granica w zerze nie istnieje⇔funkcja nie jest ciągła.
10 sie 21:42
jakubs: Dzidka, a możesz zobaczyć na mój wpis z 19:42 ? Czy jest dobrze ?
10 sie 21:55
jakubs: Wydaje mi się, że jest ok, ale wolałbym aby to ktoś potwierdził.
10 sie 22:01
Mila:
Dobrze 19:42, masz to pokazane na wykresie.
11 sie 11:02
jakubs: Dziękuję
Milu 
11 sie 11:06
jakubs: Oblicz granicę lewostronną i prawostronną w punkcie x=0
Nie wiem, czy mogę się sugerować tym, że 2
1/x<3
1/x
11 sie 11:43
Godzio:
Wczoraj miałeś podobny przykład z e
1/x 
11 sie 11:44
jakubs: Tak się nad tym zastanawiałem, ale mogę tak podzielić np. przez 3
1/x ?
11 sie 11:50
Godzio:
No a niby czemu nie

?
11 sie 11:51
jakubs: Jak widziałem 2 i 3, to tak nie bardzo myślałem, że coś się uda, gdyby były te same to tak jak
wczoraj bym podzielił.
Dzięki

11 sie 11:53
jakubs: Znowu trygonometria:
Oblicz granicę lewostronną i prawostronną w punkcie x=0
| | ⎧ | xsin1x dla −∞<x<0 | |
| f(x) | ⎩ | sin1x dla 0<x<+∞ |
|
Pierwszą wyznaczyłem i jest 0, ale tej drugiej już nie wiem jak wyznaczyć

11 sie 12:03
zombi: Druga nie istnieje
11 sie 12:13
Godzio:
| | 1 | | 1 | |
Wypada to jakoś pokazać. Niech xn = |
| oraz yn = |
| . |
| | nπ | | | |
Wówczas
Granice dla różnych pociągów są różne więc granica nie istnieje.
11 sie 12:18
jakubs: Ostatnie z granic:
Oblicz granicę lewostronną i prawostronną w punkcie x=0
11 sie 12:19
Godzio:
Bez liczenia osobno granic:
x = sgn(x) * |x| = sgn(x) *
√|x|2
| sgn(x) * √|x| | | 0 | |
| → |
| = 0 |
| √|sin(x)/x| | | 1 | |
Więc obie granice są równe 0
Licząc osobno:
Lewostronna:
| x | | −|x| | | −√x2 | |
| = |
| = |
| = ... dalej jak wyżej. |
| √−sinx | | √−sinx | | √−sinx | |
Podobnie prawostronna tylko, że minusów nie będzie
11 sie 12:46
jakubs: Rozumiem, że zamiast x podstawiłeś sgn(x)√|x|, ale czemu w mianowniku z √|sinx| zrobiło się
√|sinx/x| ?
11 sie 12:59
jakubs: ?
11 sie 23:22
Godzio: Z x zrobiłem się co innego, popatrz dokładnie, na dół wsadziłem jednego x, a drugiego
zostawiłem u góry
11 sie 23:34
jakubs: Nic z tego nie rozumiem

Chyba sobie dam siana z tym przykładem.
11 sie 23:38
Godzio:
Zobrazowanie tego co zrobiłem:
12 sie 00:08
jakubs: Mógłbym policzyć granicę kwadratu tego, a później się jakoś do tego odnieść ? Bo z tym sgn(x)
nic nie kapuje

12 sie 00:08
Godzio:
sgn(x) nam tylko znak zmienia, żeby się zgadzało z początkiem (funkcja signum)
12 sie 00:10
Godzio:
No nie wiem, czy lim f(x) = √lim f2(x)? Pewnie w większości przypadków tak, ale czy zawsze?
12 sie 00:10
jakubs:
| | −x*√−x | |
limx→0− |
| |
| | √−x*√−sinx | |
Coś takiego ?
12 sie 00:18
Godzio:
| | x2 | |
Pisałem co tam zrobiłem  |
| i teraz jednego x z góry daje na dół |
| | sinx | |
12 sie 00:28
jakubs: Jaki ze mnie tempa strzała...
Już rozumiem, dziękuję za cierpliwość. Koniec granic od Krysickiego, teraz może wezmę się za
pochodne.
12 sie 00:36
jakubs: Jeszcze z błędem napisałem

Lepiej już pójdę spać, dobranoc

12 sie 00:39
Godzio:

Pochodne będą łatwiejsze, przynajmniej samo liczenie

12 sie 01:05


 .
.
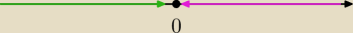 x→0−, x "idą" od lewej w stronę zera, więc są ujemne tak? Natomiast x→0+, czyli x "idą od
prawej strony do zera, więc są dodatnie, prawda?
Zielone: x→0−
Fioletowe: x→0+
Skoro wiesz jakie będą przyjmowały wartości (ujemne/dodatnie) te nasze iksy, wiesz już jak
opuszczać moduł z mianownika, czy ze znakiem + czy ze znakiem −
x→0−, x "idą" od lewej w stronę zera, więc są ujemne tak? Natomiast x→0+, czyli x "idą od
prawej strony do zera, więc są dodatnie, prawda?
Zielone: x→0−
Fioletowe: x→0+
Skoro wiesz jakie będą przyjmowały wartości (ujemne/dodatnie) te nasze iksy, wiesz już jak
opuszczać moduł z mianownika, czy ze znakiem + czy ze znakiem −
 Granica w zerze nie istnieje⇔funkcja nie jest ciągła.
Granica w zerze nie istnieje⇔funkcja nie jest ciągła.



 ?
?


 Chyba sobie dam siana z tym przykładem.
Chyba sobie dam siana z tym przykładem.


 Lepiej już pójdę spać, dobranoc
Lepiej już pójdę spać, dobranoc 
 Pochodne będą łatwiejsze, przynajmniej samo liczenie
Pochodne będą łatwiejsze, przynajmniej samo liczenie 