proszę o rozwiązanie proszę o rozwiązanie: rozwiąz równanie tg2x + tgx −1 = ^sin2x₂( 1 + sin²x + sin⁴x + sin⁶x + ....) wiem że jest to ciag ale nie wiem jak się do tego zabrać próbowałem rozpisać lewą stronę ale nic z tego nie wyszło wynik to x = ^π₈ + uk{π}{2} , k ∊ C

Eta: Ze względu na tangens : cosx≠0 ⇒ x≠.......... 1+sin²x+sin⁴x+.... −−− ciąg geometryczny a₁=1 q= sin²x , sinx≠0 ⇒ x≠ ......... Suma tego ciągu jest zbieżna gdy : |q|<1 ⇒ |sin²x|<1 ⇒ ..............

	a1		1		1
S=		=		=
	1−q		1−sin2x		cos2x

zatem równanie przybiera postać:

	2sinx*cosx		1
tg(2x)+tgx−1=		*
	2		cos2x

	π		π
tg(2x)+tgx−1= tgx ⇒ tg(2x)= 1 ⇒ ......... x=		+k*		, k∊C
	8		2

Eta: Poprawiam zapis : 1+sin²x+sin⁴x −−− suma ciągu geometrycznego

pigor: ..., ciąg sum częściowych nieskończonego ciągu geometrycznego

	a1
(krótko − szereg geometryczny) zbieżny, gdy |q|<1 do liczby S=		.. .
	1−q

Eta:

proszę o rozwiązanie: bardzo dziękuję moj błąd polegał na tym że rozwiązywałem lewą stronę rownania

tyu: @ proszę o rozwiązanie z jakiego zbioru jest ten przykład

5-latek: tyu takie zadania sa w kazdym zbiorze zadan z przed reformy (tzn chyba do 2002r ) Ale nie wiem czy teraz w programie sa ciagi geometryczne nieskonczoone jesli tak to zobacz w ktorej klasie to jest i znajdz sobie jakis zbior do tej klasy . Moze Pazdro

proszę o rozwiązanie: jest to zadanie ze zbioru zadań dla kl2 kurczab wyd 2013 mam jeszcze problem z zadaniem wyznacz wartości parametru k k∊ R dla ktorych równanie (sinx − cosx) ( sinx + 0,5k) =0 ma cztery różne rozwiązania w przedziale ≤0, ^3π₂≥ wynik to k ∊ ( −2, √2) ∪ ( − √2 , 0) ja to zacząłem rozwiązywać tak (sinx − cosx) =0 lub (sinx + 0,5)=0 sinx = − 0,5 ⇒ x=^π₆ +2kπ sinx− sin(^π₂ − x ) = 0 po zastosowaniu wzoru sin(x +^π₄)= 0 ⇒ x = ^3π₄ + 4kπ ale chyba moje rozumowanie jest nieprawidłowe

tyu: dzięki. widzę. ostatnia strona tego tematu.

Mila:

	1
sinx−cosx=0 lub sinx=−		k
	2

sinx=cosx /:cosx lub (sinx= ... to rozważymy później) tgx=1 ( mogłeś podzielić bo cosx≠0, gdyby cosx=0, to sinx≠0 i równanie nie jest spełnione)

	π		π		5π
x1=		lub x2=		+π=
	4		4		4

	3π
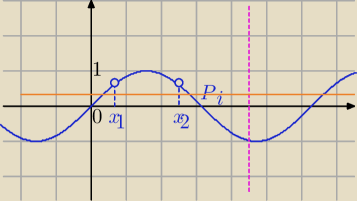
Zobaczymy jak wygląda wykres sin(x) w przedziale <0,		>,
	2

Mamy tam juz dwa rozwiązania, Aby otrzymać jescze dwa różne rozwiązania równania

	1
sinx=−		k to
	2

Pomarańczowa prosta musi przeciąć wykres sinusa w dwóch punktach różnych od zaznaczonych

	1		1		√2
⇔0≤−		k<1 i −		k≠		⇔
	2		2		2

0≥k>−2 i k≠−√2 dla k=0 mamy sinx=0 to cosx≠0 i pierwsze równanie nie jest spełnione ⇔k∊(−2,−√2)∪(−√2,0)

proszę o rozwiązanie: dziękuję

proszę o rozwiązanie: następne zadanie jest podobne iznów robię jakiś błąd wyznacz wartości parametru m m ∊ R dla kyórych równanie (2cosx − 1 ) (sinx − m ) = 0 ma cztery różne rozwiązania w przedziale ≤ − ^π₂ , ^3π₂ ≥ z których trzy są dodatnie wynik to m∊ (0, ^√3₂ ) ∪ ( ^√3₂, 1) 2cosx =1 ⇒ cosx = ¹₂ ⇒ x = ^π₃ lub sinx = m − ^π₂≤ m ≤ ^3π₂ coś znowu robię żle

Mila:

	1
cosx=
	2

	π		−π
x1=		lub x2=
	3		3

sinx=m i masz mieć jeszcze 2 dodatnie rozwiązania, popatrz na wykres f(x)=sinx

	√3		π
0<m<1 i m ≠		, bo sin		musimy pominąć, tam pierwsze równanie ma dodatnie
	2		3

rozwiązanie.⇔

	√3		√3
m∊(0,		)∪(		,1)
	2		2

Mam trudności z rysunkiem, coś ta opcja źle działa, może w innym wpisie uda się.

proszę o rozwiązanie: dziękuję bardzo