calki obliczyć Matstud: ∫∫|cos(x+y)|dxdy gdzie D=[0,π]x[0,π]

Kacper: zamień na całki iterowane

Matstud: tzn jak

Godzio:

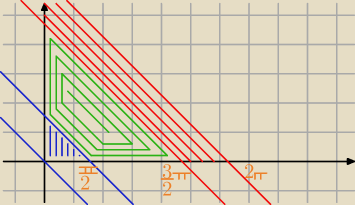
	π		3
cos(x + y) ≥ 0 gdy x + y ∊ [0,		] U [		π,2π]
	2		2

	π		3
cos(x + y) < 0 gdy x + y ∊ (		,		π)
	2		2

Oraz x ∊ [0,π] i y ∊ [0,π]

	π
0 ≤ x + y ≤
	2

	π
−x ≤ y ≤ − x +
	2

	3
−x +		π ≤ y ≤ −x + 2π]]
	2

	π		3
−x +		π < y < −x +		π
	2		2

Teraz napisz całki po tych obszarach. Niebieski i czerwony − cos(x + y) jest dodatni, zielony − cos(x + y) jest ujemny. Początek jest łatwy, zielony obszar trzeba podzielić na dwie całki. ∫∫|cos(x + y)|dxdy = ... + ∫₀^π/2∫_{−x + π/2}^{−x + 3π/2}(−cos(x + y))dydx + ∫_π/2^3π/2∫₀^{−x + 3π/2}(−cos(x + y))dydx + ... Czerwony obszar podobnie.

b.: łatwiej zamienić na całki iterowane: I = ∫₀^π ( ∫₀^π |cos(x+y)| dx) dy = ∫₀^π ( ∫_y^π+y |cos(x)| dx) dy Ponieważ funkcja x −> |cos(x)| jest π−okresowa, więc wewnętrzna całka jest taka sama, jak całka po odcinku [−π/2, π/2], czyli I = ∫₀^π ( ∫_−π/2^π/2 |cos(x)| dx) dy = ∫₀^π ( ∫_−π/2^π/2 cos(x) dx) dy = ∫₀^π 2 dy = 2π.