f.kwadratowa tyu: Zbadaj liczbę rozwiązań w zależności od parametru m. (m−3)x² + (m−2)x + 1 = 0 I − jeśli jest m−3=0 m=3 to jest f. liniowa. II − jeśli jest m∊R− {3}, to mam f. kwadratową i rozpatruję liczbę rozwiązań w zależności od m. Δ=(m−2)²−4(m−3)=m²−8m+16 Δ=m²−8m+16 m₀=4 Δ_m=(m−4)² Dlaczego tutaj może być tylko taki przypadek, że jest 1/ jedno rozwiązanie albo 2/ są dwa rozwiązania Czy chodzi o to, że funkcja k=m²−8m+16 ma tylko jedno miejsce zerowe i jest nad OX. http://www.matemaks.pl/program-do-rysowania-wykresow-funkcji.php?funkcja=x^2-8x%2B16&dokladnosc=100&skala=40.00

J: Dla m ≠ 3 funkcaj ma 2 pierwiastki, gdy Δ > 0 oraz 1 pierwiastek, gdy Δ = 0 Tutaj masz: Δ = (m−4)² , a więc dla m ≠ 4 i m ≠ 3 − dwa rozwiązania , dla m = 4 i m = 3 − jedno rozwiązanie.

J: Ta funkcja zawsze ma jedno lub 2 rozwiązania, bo Δ nigdy nie jest ujemna ..

Janek191: Δ = m² − 8 m + 16 = ( m − 4)² Dla m = 4 jest Δ = 0 − jedno rozwiązanie Dla m ≠ 4 jest Δ > 0 − są dwa rozwiązania

tyu: rozumiem, ale dlaczego nie rozpatruje się przypadku (m−4)²< 0

Janek191: Poprawka: Dla m ≠ 4 i m ≠ 3 − są dwa rozwiązania

Janek191: Bo ( m − 4)² ≥ 0 dla m ∊ℛ

tyu: ale dlaczego Δ nigdy nie jest ujemna Bo wykres y=( m − 4)² nigdy nie będzie pod OX

tyu: aha. No to teraz rozumiem. Czyli chodzi o to, że ( m − 4)² ≥ 0 dla m ∊ℛ, dlatego może być albo jedno rozwiązanie albo dwa rozwiązania. Dziękuję za pomoc.

J: Janku ... dla m = 3 też jest jedno rozwiazanie : x = −1

Janek191: Napisałem wyżej Δ = ( m − 4)² ≥ 0 Dla m = 4 jest Δ = 0, a dla m ≠ 4 jest Δ > 0

Janek191: Ja pisałem do II i dlatego tak wyszło

J: Zgoda..., ale tylko ze względu na Δ , a zadanie ma szerszy zakres , parametr m nie tylko dla Δ, ale dla całego równania. Jeśli da odpowiedź : dla m = 4 jest jedno rozwiązanie to pominie m = 3

J: Wiem Janek .... Pozdrawiam...

tyu: znów nie rozumiem jednej rzeczy I − gdy jest jedno rozwiązanie, to Δ=0 czyli (m−4)²=0 ⇒ m=4 ale dlaczego aby było jedno rozwiązanie, to dodatkowo jest warunek m=3 Bo jeśli wpiszemy, że m=3, to zrobi się f. liniowa. Chyba że o to chodzi, by powstała f. liniowa Czy nie wyrzuca się ze zbioru m liczby 3, bo ona zeruje współczynnik "a" i robi się f. liniowa

MQ: Właśnie o to chodzi.

J: O Twoim równaniu ( jego postaci ) decyduje parametr m. Gdy m = 3 ,Twoje równanie staje się równaniem liniowym i ma jedno rozwiązanie.

tyu: to po co wyrzuca się m=3 w przypadku nr I

J: A kto Ci powiedział,że się wurzuca ?

tyu: już chyba zaczynam rozumieć. Jeśli jest polecenie dotyczące określenia liczby rozwiązań ze względu na parametr m, no i zbiór rozwiązań, w którym równanie ma jedno rozwiązanie składa się: 1/ takiego m, które zeruje współczynnik "a" i z f. kwadratowej robi się liniowa, 2/ takich m, dla których Δ=0 Czy tak to się rozwiązuje

J: Masz polecenie. zbadaj ilość rozwiązań... Rozpatrujesz 2 przypadki: A) a = 0 , czyli : (m = 3) .... równianie staje się równaniem liniowym − 1 rozwiązanie B) a ≠ 0 , czyli : (m ≠ 3) ...równianie staje się równaniem kwadratowym: Dla Δ >0 − 2 pierwiastki Dla Δ = 0 − 1 pierwiastek Dla Δ < 0 − brak pierwiatków Tearz sumujesz te dwa przypadki: Dla m = 4 ( Δ=0) oraz m = 3 (funkcja liniowa) − 1 rozwiazanie Dla m ≠ 4 (Δ>) oraz m ≠ 3 (funkcja kwadratowa) − 2 rozwiązania ..... koniec zadania.

tyu: dziękuję za wyjaśnienie. Może w końcu to zrozumiem.

tyu: Proszę o sprawdzenie. Zbadaj liczbę rozwiązań w zależności od parametru m. (m−3)x² + (m−2)x + 1 = 0 A/ gdy a=0, to jest f.liniowa, więc jest jedno rozwiązanie F. liniowa powstaje zatem dla m−3=0, więc dla m=3 jest jedno rozwiązanie. B/ gdy a≠0 to powstaje f. kwadratowa. gdy m−3≠0 więc dla m≠3 jest f. kwadratowa Δ=m²−8m+16 (m − 4)² ≥ 0 dla m ∊R dlatego sprawdzam tylko przypadki Δ>0 −−− 2 rozwiązania Δ=0 −−−− 1 rozwiązanie 1/ Δ>0 −−−−−−−−−− 2 rozwiązania m≠3 (warunek istnienia f. kwadratowej) (m − 4)² >0 ⇒ m∊R / {4} czyli 2 rozwiązania są dla m∊R / {3;4} 2/ Δ=0 −−−− 1 rozwiązanie Δ=(m−4)² = 0 , więc m=4 Ale równanie (m−3)x² + (m−2)x + 1 = 0 dla m=3 przyjmuje postać f.liniowej, w której też ma jedno rozwiązanie. Zatem jedno rozwiązanie jest dla m={3;4} Czy tak to ma wyglądać Tylko się zastanawiam dlaczego, licząc pkt 2 (Δ=0 czyli 1 rozwiązanie f.kwadratowej), nie uwzględnia się tego, że jeśli m=3, to będzie to f. liniowa, więc po co liczyć Δ i porównywać ją do zera, skoro f.liniowa delty nie ma?

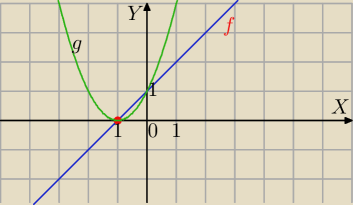
Mila: 1) Jeśli m=3 to mamy równanie: 0*x²+(3−2)*x+1=0 x+1=0 x=−1 f(x)=x+1 2)m=4 Masz równanie: x²+2x+1=0 (x+1)²=0 x=−1 g(x)=(x+1)² Masz dwie różne funkcje.

tyu: dziękuję za wyjaśnienie