czy ktoś mo ze to sprawdzić proszę o rozwiązanie: rozwiąż rownanie cos²x + cos³x + cos⁴x + cos⁵x + ...... ≥ 1 + cosx moje rozwiązanie to a₁ = cos²x q = cosx I cosxI <1 S = ^cos2x_{1− cosx} ^cos2x_{1− cosx} ≥ 1+ cosx po przekształceniu mamy ( 2 cos²x −1) ( 1 − cosx ) ≥ 0 cosx = ^p{2₂ lub cosx = − ^p{2₂ lub cosx =1 ⇒ x ≠ 2kπ ∉ D x =^π₄ + 2kπ lub x = − ^π₄ + 2kπ ale w odpowiedż jest taka x =^π₄ + kπ lub x = − ^π₄ + kπ lub x ≠ kπ ∉ D dlaczego

ICSP: równanie, nierówność, z czym w końcu mamy do czynienia ?

proszę o rozwiązanie: rzeczwiście polecenie jest rozwiąż nierówność a wynik zapisany jest < − ^π₄ + kπ , kπ) ∪ ( kπ, ^π₄ + kπ ≥

ICSP: D : cosx ≠ ± 1 ( x ≠ kπ) (2cos²x − 1)(1 − cosx) ≥ 0 // : 1 − cosx > 0 2cos²x − 1 ≥ 0 2cos²x − cos²x − sin²x ≥ 0 cos²x − sin²x ≥ 0 cos2x ≥ 0

ICSP: teraz narysuj wykres cos(2x) i z niego odczytaj zbiór rozwiązań, pamiętając o dziedzinie.

proszę o rozwiązanie: dziękuję ale czy moje rozwiązanie jest błędne

ICSP:

	√2
a gdzie są rozwiązania dla cosx = −		?
	2

proszę o rozwiązanie: słusznie dla cosx = − ^√2₂ x = ⁵₄ + 2kπ ≠ D

wmboczek: chyba w odpowiedzi nie uwzględnili przypadku cosx=−1 i wycięli wszystkie kπ zamiast parzystych

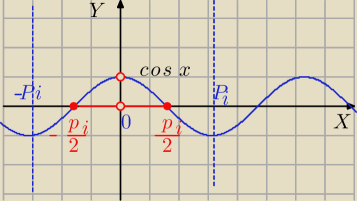
Mila: 1) |cosx|<1⇔ −1<cosx<1⇔ x≠kπ, k∊C 2) cos(2x)≥0 i x≠kπ

	π		π
−		+2kπ≤2x<0+2kπ lub 0+2kπ<2x≤		+2kπ /:2
	2		2

	π		π
−		+kπ≤x<kπ lub kπ<x≤		+kπ⇔
	4		4

	π		π
x∊<−		+kπ,kπ)∪(kπ,		+kπ>
	4		4

Mila:

proszę o rozwiązanie: DZIĘKUJĘ

Mila: Zrozumiałeś teraz odpowiedź?

proszę o rozwiązanie: oczywiście jeszcze raz dziękuję