aa Hugo: wymierne: (naszkicuj wykres funkcji)

	2x−|x+1|
f(x)=		, dziedzina = R\{1}
	x−1

Rozbilem sb na dwie równośći x≥0 oraz x<0

2x−x−1
x−1

f stała y=1

2x+x+1
x−1

3x+1
x−1

3x−6+5
x−1

	5
3 +
	x−1

Stosujemy te wszystkie rachunki by nie szukać dla każdego x odpowiadającą mu wartość tworząc żmudne zadanie. Jednak odpowiedź jest inna:

	5
3 +		dla x< −1
	x−1

1 dla x≥0 /{1} Dlaczego funkcja rozszczepia się na dwa segmenty w pkt x=−1 ma to związek z wartością wzgl |x+1|?

Hugo: tam mam błąd

	5
3 +		dla x< −1
	x−1

1 dla x≥−1 /{1}

Mila: D=R\{1} 1) |x+1|= x+1 dla x+1≥0⇔x≥−1 2) |x+1|=−x−1 dla x<−1 w tych dwóch przedziałach rozważasz f(x) opuszczając znak wartości bezwzględnej.

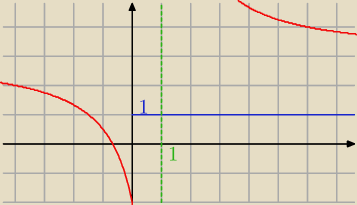
PW: Idzie o to, że funkcja nie ma żadnej wartości dla x=1 (nie ma tam dziedziny), więc kreska y=1 ma "puste kółko" w (1,1). A ten czerwony kawałek wykresu w pierwszej ćwiartce nie powinien być narysowany (skąd się to wzięło?).

Hugo: racja... ale ja sie cofam ;x dziękuję Milo

Hugo: czerwony kawalek jest tylko taki se bo wklepałem funkcje by mi narysowalo a nie ma tam chyba opcji ze dla x<−1

Mila: Czy mam narysować?

tyu: @ Hugo − poprawiasz maturę, bo to chyba zdanie maturalne raczej, czy może to zadanko z myślą o studiach

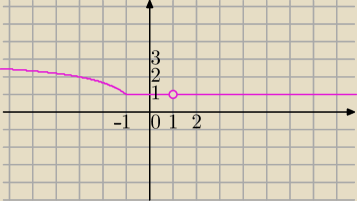
Mila: f(x)=1 dla x≥−1 i x≠1

	4
f(x)=3+		dla x<−1
	x−1

PW: Hugo daje świadectwo cudu − po zdaniu matury wszystko cudownie zapomniał.

Hugo: Hugo daje jutro korki z wielomianów a potem wymierne

tyu: czyli odpalasz procent dla każdego kto przyczynił się do wyjaśnienia Ci tego zadania

Hugo: wolontariat, jak chcecie a sie spisze to wam mogę dać po buziaku jak dostanę jutro.

tyu: czyli działasz pro publico bono. To się chwali.