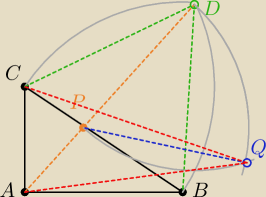
 ABC jest trójkątem prostokątnym o kącie prostym przy A, oraz |AB| > |AC|. Punkt D jest
zdefiniowany tak że trójkąt BCD jest równoboczny oraz AD przecina BC w P. Punkt Q jest
zdefiniowany tak że trójkat QDP jest równoboczny oraz QP przecina DB. Pokaż że |QA| < |QC|.
Znalazłem na innym forum
ABC jest trójkątem prostokątnym o kącie prostym przy A, oraz |AB| > |AC|. Punkt D jest
zdefiniowany tak że trójkąt BCD jest równoboczny oraz AD przecina BC w P. Punkt Q jest
zdefiniowany tak że trójkat QDP jest równoboczny oraz QP przecina DB. Pokaż że |QA| < |QC|.
Znalazłem na innym forum  Mam prawie całe rozwiązanie, tylko zostało mi porównać pewne dwa kąty i zatrzymałem się.
Może ktoś ma jakiś pomysł na rozwiązanie?
Mam prawie całe rozwiązanie, tylko zostało mi porównać pewne dwa kąty i zatrzymałem się.
Może ktoś ma jakiś pomysł na rozwiązanie? 

 A
A

 Ponoć tylko zatrzymał się ... na chwilkę ...
Ponoć tylko zatrzymał się ... na chwilkę ...



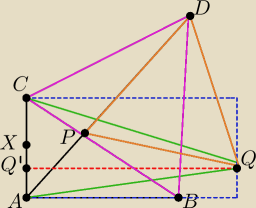 ja bym kombinował z tym że punkt Q (Q') musi leżeć na odcinku AX, gdzie X jest środkiem boku AC
ja bym kombinował z tym że punkt Q (Q') musi leżeć na odcinku AX, gdzie X jest środkiem boku AC


 geogebra mówi coś innego xd
geogebra mówi coś innego xd
 A co mówi Ci geogebra ?
A co mówi Ci geogebra ?







 rozwali nam to zadanie
rozwali nam to zadanie 

 .
.

 .
Eta, pomysł na mój nik wziął się z zachowania mojej sąsiadki, dzisiaj starszej już Pani, z
lat mojego dzieciństwa. Zawsze mówiła na mnie Ajtek. Mało tego, zostało tak do dzisiaj, a nie
ma problemu z wymawianiem litery "r"
.
Eta, pomysł na mój nik wziął się z zachowania mojej sąsiadki, dzisiaj starszej już Pani, z
lat mojego dzieciństwa. Zawsze mówiła na mnie Ajtek. Mało tego, zostało tak do dzisiaj, a nie
ma problemu z wymawianiem litery "r"  .
.
 a nam zostawił główkowanie
a nam zostawił główkowanie 
 Życzę sukcesu.
Życzę sukcesu.
 Co do pierwszego pomysłu Ety, to trójkąt ABC nie jest 30,60,90 bo tylko mamy informacje o
tym, że nie jest równoramienny
Co do pierwszego pomysłu Ety, to trójkąt ABC nie jest 30,60,90 bo tylko mamy informacje o
tym, że nie jest równoramienny 
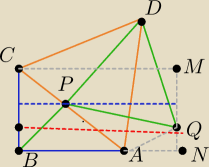 Dla równoramiennego ABC kąt DPA =90, czyli QP jest nachylony pod kątem 30 do boku CA. Na AQDP
można opisać okrąg, więc kąt PAQ =120, wtedy PQA =30. CAB=45, QAN=15, AQN=75 czyli PQM =75. Z
tego wynika ,że dla równoramiennego punkt Q leży poniżej połowy NM, czyli CQ jest większe od
QB. Gdy BA jest większe od CB kąt DPQ jest mniejszy od 90( środek CA , nazwijmy go X, jest
poniżej P, a DXP jest prosty), czyli zmniejsza się też kąt nachylenia PQ, więc tym bardziej
zachodzi teza
Dla równoramiennego ABC kąt DPA =90, czyli QP jest nachylony pod kątem 30 do boku CA. Na AQDP
można opisać okrąg, więc kąt PAQ =120, wtedy PQA =30. CAB=45, QAN=15, AQN=75 czyli PQM =75. Z
tego wynika ,że dla równoramiennego punkt Q leży poniżej połowy NM, czyli CQ jest większe od
QB. Gdy BA jest większe od CB kąt DPQ jest mniejszy od 90( środek CA , nazwijmy go X, jest
poniżej P, a DXP jest prosty), czyli zmniejsza się też kąt nachylenia PQ, więc tym bardziej
zachodzi teza

| c√3 | ||
jeżeli CD=c i PQ=d to wysokość opuszczona z punktu Q na CD jest równa | ||
| 2 |
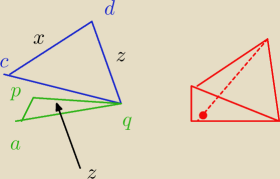 z pitagorasa x2 = |ac|2 + |ab|2
z< x
Mi tylko brakuje zależności w połączeniu wierzchołków trójkąta równobocznego z tr.
prostokątnym.
Powinny być wzory na to : > (?) (czerwony rysunek)
z pitagorasa x2 = |ac|2 + |ab|2
z< x
Mi tylko brakuje zależności w połączeniu wierzchołków trójkąta równobocznego z tr.
prostokątnym.
Powinny być wzory na to : > (?) (czerwony rysunek)
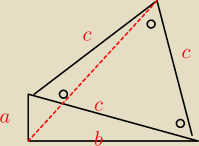 O te zależności sie rozbija cały czas
O te zależności sie rozbija cały czas  i to by nam duzo dało jak by ktoś znalazł albo
wiedział
http://www.wielokat.pl/twierdzenie-menelaosa/
twierdzenie menelaosa potem tez mozna uzyc
i to by nam duzo dało jak by ktoś znalazł albo
wiedział
http://www.wielokat.pl/twierdzenie-menelaosa/
twierdzenie menelaosa potem tez mozna uzyc
 ?
?
 To raczej zadanie olimpijskie
To raczej zadanie olimpijskie  Chyba wrzucę je na forum, gdzie ludzie są na bieżąco z taką tematyką tylko muszę podszkolić mój
angielski
Chyba wrzucę je na forum, gdzie ludzie są na bieżąco z taką tematyką tylko muszę podszkolić mój
angielski 
 ew. na jakiegós
mathlinks (AoPSa). Ale na matematyka.pl powinni dać radę.
ew. na jakiegós
mathlinks (AoPSa). Ale na matematyka.pl powinni dać radę.
 myślałem o mathlinksie wcześniej i tam wrzucę
myślałem o mathlinksie wcześniej i tam wrzucę 

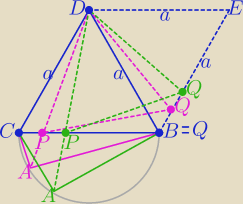 Proponuję spróbować tak spojrzeć na podany w zadaniu problem:
Każdy z wierzhołków A trójkątów prostokątnych ABC o kącie prostym przy wierzchołku A leży na
łuku półokręgu o średnicy BC. Punkt P leży na tej średnicy BC.
Trójkąt BDE jest równoboczny i przystający do trójkąta równobocznego CBD. Czworokąt
CBED jest rombem o kącie ostrym o mierze 60o (są to jakby sklejone dwa trójkąty
równoboczne).
Trzeba najpierw wykazać, że wierzchołek Q trójkata rownobocznego PQD leży na boku BE trójkąta
BDE (pomoże tu spostrzeżenie Saizou o trapezie z 12 sierpnia godz. 17:24).
Punkt A przesuwając się po łuku półokręgu powoduje przesunięcie punktu P na średnicy BC
i punktu Q na odcinku BE.
Proponuję spróbować tak spojrzeć na podany w zadaniu problem:
Każdy z wierzhołków A trójkątów prostokątnych ABC o kącie prostym przy wierzchołku A leży na
łuku półokręgu o średnicy BC. Punkt P leży na tej średnicy BC.
Trójkąt BDE jest równoboczny i przystający do trójkąta równobocznego CBD. Czworokąt
CBED jest rombem o kącie ostrym o mierze 60o (są to jakby sklejone dwa trójkąty
równoboczne).
Trzeba najpierw wykazać, że wierzchołek Q trójkata rownobocznego PQD leży na boku BE trójkąta
BDE (pomoże tu spostrzeżenie Saizou o trapezie z 12 sierpnia godz. 17:24).
Punkt A przesuwając się po łuku półokręgu powoduje przesunięcie punktu P na średnicy BC
i punktu Q na odcinku BE.