Funkcja liniowa
Blue: Uzasadnij, że jeśli prosta nie jest równoległa do osi OY, to jej równanie można zapisać w
postaci:
gdzie (x
1,y
1) i (x
2,y
2) są dowolnymi, różnymi punktami należącymi do tej prostej

6 sie 18:19
Mila:
y=ax+b, równanie kierunkowe prostej.
6 sie 18:45
MQ: Albo tak:
Lewa i prawa stona równania to tg kąta nachylenia odcinka o początku w p. (x1,y1) i końcach:
(x,y) − lewa i (x2, y2) − prawa.
A zatem oba odcinki są równoległe i zaczepione w p. (x1,y1), czyli każdy punkt (x,y) jest
współliniowy z punktami (x1,y1) i (x2, y2).
6 sie 18:50
Bury:
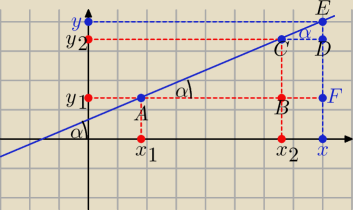
A(x
1, y
1), B(x
2, y
1), C(x
2, y
2), D(x, y
2), E(x, y), F(x, y
1)
|AB| = x
2 − x
1, |BC| = y
2 − y
1, |CD| = x − x
2, |DE| = y − y
2, |AF| = x − x
1,
|FE| = y − y
1
| | |BC| | | |DE| | |
Z podobieństwa trójkątów ABC i CDE: = |
| = |
| |
| | |AB| | | |CD| | |
| | y2 − y1 | | y − y2 | |
stąd |
| = |
| |
| | x2 − x1 | | x − x2 | |
albo
| | |BC| | | |FE| | |
z podobieństwa trójkątów ABC i AFE: = |
| = |
| |
| | |AB| | | |AF| | |
| | y2 − y1 | | y − y1 | |
stąd |
| = |
| |
| | x2 − x1 | | x − x1 | |
6 sie 19:12
Eta:
k: y=ax+b i A(x
1,y
1)≠ B(x
2, y
2) ∊k
→
AB= [x
2−x
1, y
2−y
1]
| | y2−y1 | |
a= tgα= |
| i A(x1,y1) |
| | x2−x1 | |
| | y2−y1 | |
k: y= |
| (x−x1) +y1 |
| | x2−x1 | |
| | y2−y1 | |
k: y−y1= |
| (x−x1) |
| | x2−x1 | |
| | y−y1 | | y2−y1 | |
k: |
| = |
| |
| | x−x1 | | x2−x1 | |
6 sie 19:36
pigor: ... lub np. tak
y=ax+b i y1=ax1+b i y2=ax2+b /−stronami (1)−(2)
i (3)−(2) ⇒ y−y
1= a(x−x
1) i y
2−y
1= a (x
2−x
1) ⇒
| | y−y1 | | y2−y1 | | y−y1 | | y2−y1 | |
⇒ a= |
| i a= |
| ⇒ |
| = |
| .  |
| | x−x1 | | x2−x1 | | x−x1 | | x2−x1 | |
6 sie 23:46
:\:
6 sie 23:49
Bury:
W tym uzasadnieniu nie można korzystać z wzoru y = ax + b, bo jest to inna postać wzoru,
który trzeba uzasadnić, to takie masło maślane.
7 sie 00:08
pigor: .., nie zgadzam się, bo y=ax+b i a≠0 to pełnoprawna część założenia −
− równanie prostej nie równoległej do OY, które spełniają 2 dane punkty.
−−−−−−−−−−−−−−−−−−−−−−−
zgodzić się jedynie mogę z faktem, że nie napisałem warunku a≠0 i to tyle.
7 sie 00:25
Blue: Pigor, Twój sposób jest najlepszy, dzięki!

9 sie 15:03

 A(x1, y1), B(x2, y1), C(x2, y2), D(x, y2), E(x, y), F(x, y1)
|AB| = x2 − x1, |BC| = y2 − y1, |CD| = x − x2, |DE| = y − y2, |AF| = x − x1,
|FE| = y − y1
A(x1, y1), B(x2, y1), C(x2, y2), D(x, y2), E(x, y), F(x, y1)
|AB| = x2 − x1, |BC| = y2 − y1, |CD| = x − x2, |DE| = y − y2, |AF| = x − x1,
|FE| = y − y1

