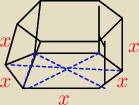
aa Hugo: Betonowa kostka ma kształt graniastosłupa, którego podstawą jest 6−kąt foremny. Oblicz wysokość tego graniastosłupa, jeśli jego objętość jest równa 6√3dm³ rys. rozw: V=pp*H

	x2√3
6√3 = 6*		* x
	4

	x2
1=		* x
	4

4=x³ x= ³√4 Prosze mi to sprawdzic nie mam odpowiedzi, a dziwny jest wynik

pazdro: Pionowo kresek nie dało sie narysować?, trochę staranności by sie przydało w tym, co się prezentuje publicznie.

Saizou :

	x2√3		3
Pp=6*		=		x2√3
	4		2

H=? V=P_p*H

	3
6√3=		x2√3*H
	2

12√3=3x²√3H 4=x²H

	4
H=
	x2

pazdro: A skąd wiadomo, że wysokość graniastosłupa jest równa długości krawędzi podstawY?

Hugo: z rysunku

pazdro: z jakiego rysunku?

Hugo: Saizou H = x

	4
H=
	x2

	4
x=
	x2

x³=4 ... i to co u mnie

Hugo: tego w książcce a w konsekwencji tego co wklepałem tu na forum : )

Hugo: dziękuje Saizou

5-latek: pazdro Pani prof. Krygowska w swojej ksiazce do geometrii do klasy 1 liceum piszsse tak. [P[Niedokladnosci rysunku nie wprowadzaja nas w blad jesli pamietamy ze przedmiotem naszego rozumowania jest figura pomyslana a nie wykreslona]] Oczywiscie starannie wykonany rysunek moze w wielu przypadkach ulatwic rozumowanie . Pamietac jednak musimy ze rysunek jest tylko czescia tgo czym sie zajmujemy ,oraz ze przedstawia pomyslane figury w spposob umowny . Poa tym czasami jest tu zle rysowac i nie czepiajmy sie tego ze ktos narysuje krzywo kreske . Betonowa kostka kazdy wie jak wyglada . Prawie wszyscy maja ja przed domem lub garazem wylozona

Hugo: Jutro Huguś daje korypetycje z wielomianów

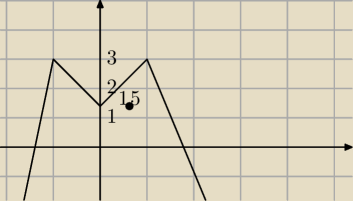
Hugo: pomóżcie mi jeszcze bo nie wiem : > przykładowy wykres: podaj liczbę rozwiązań równania w zależności od parametru m i mam w(x)=|m| i jak mam to rozumieć ? dla m=3 oraz m e (3; 2) u (1,5 ; 0] , 2 rozw dla m=2 , 3 rozw dla m>3 , 0 rozw a to poniżej jak mam |m| to jak to sie?

pazdro: Niechlujstwo, to niechlujstwo i nie można takiej postawy usprawiedliwiać. Czym skorupka nasiąknie w okresie uczenia się, tym później trąci. A tu rysuje sie bardzo łatwo, kratki się wyświetlają i pionowe kręski, połaczenia odcinków i inne elementy rysunku można tu bez bez problemu wykonać. Trzeba, tak jak we wszystkich poczynaniach, włozyć w swoją pracę trochę wysiłku.

Hugo: ktos pomoze ?

Mila: 1) czy to wykres w(x)?

Mila: 2) o jakie równanie chodzi?

Hugo: tak

Hugo: po prostu to jest taka funkcja pokazana na wykresie i mamy odczytać ilośc rozwiązań względem parametru m w(x)=|m| dla w(x)=m jest prosto , umiem ale jak widze wartość względną to nie wiem jak zrobic

Kacper: to zrób dla k=|m| a potem z tego policz m

Hugo: a mozesz od razu ;x? bo nie jestem z tym pewny

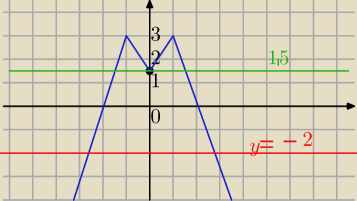
Mila: 1) liczba rozwiązań równania w(x)=m rysujesz poziomą linię i przesuwasz np. od dołu do góry. a) Dla m∊(−∞,1.5) masz 2 rozwiązania b) dla m=1.5 są trzy rozwiązania c) dla m∊(1.5, 3) są 4 rozwiązania d) dla m=3 są dwa rozwiązania e)m∊(3,∞) brak rozwiązań. 2) liczba rozwiązań równania w(x)=|m| Ponieważ |m|≥0 to a) są dwa rozwiązania dla 0≤|m|<1.5 ⇔|m|<1.5⇔m∊(−1,5; 1,5) b) są 3 rozwiązania dla |m|=1.5 czyli dla m=−1.5 lub m=1.5 c)są 4 rozwiązania dla |m|∊(1.5;3) czyli 1,5<|m|<3⇔ rozwiąż i sprawdź w wolf. d) są 2 rozwiązania dla |m|=3 ⇔m=−3 lub m=3 e) |m|>3 ⇔m<−3 lub m>3 brak rozwiązań.

Hugo: http://scr.hu/2pdc/v30j8 wykres.. już zacząłem przepisywac całe polecenie od nowa :x Hmmm Milo dziękuję ! już patrzę

Mila: No to jest trochę inny wykres. Hugo zamiast 1.5 masz tam 1 wpisać.

Hugo: oczywiście ! tak tak dziękuje Milo

Hugo: okej rozumiem twoje i cofam to swoje nowe dziwne ! 0≤|m| <====== to sie równa 0 prawda ?

Hugo: nein ! 0≤|m| m ∊ R a zatem mi sie koliduje z tym "są dwa rozwiązania dla 0≤|m|<1.5 ⇔|m|<1.5⇔m∊(−1,5; 1,5)" moze ktos mi to rozjasnic

Mila: |m|≥0 dla każdego m z definicji wartości bezwzględnej. Stąd nie będzie równa wartości ujemnej w(x) ( wykres pod osią) |m|=0 dla m=0

Mila: m=0 jest w przedziale (−1,5; 1.5)

Hugo: musze to jeszcze przeanalizowąc ehmmm ; / dziękuje za cierpliwosc !

Mila: Skąd to zadanie?

Hugo: wiec:Matematyka nowej ery ale nowa postawa

Mila: Dziękuję . Najczęściej pytali o liczbę rozwiązań równania |f(x)|=m