trygonometria tyu: jeśli w zadaniu, które jest tu http://forum.zadania.info/viewtopic.php?f=24&t=19213 oznaczone jako 3a) log_√2sinx (1+cosx)=2

	π		3π
mam dziedzinę Df: x∊(2kπ; 2kπ+π) / {		+ 2kπ;		+ 2kπ }
	4		4

	−π
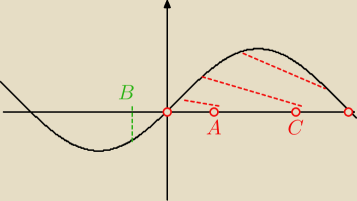
to dlaczego		+ 2kπ nie należy do dziedziny
	3

	−π
rys. B=		+ 2kπ
	3

	π
A=		+ 2kπ
	4

	3π
C=		+ 2kπ
	4

	−π
czy chodzi o to, że B=		+ 2kπ jest poniżej OX
	3

Eta: tak

tyu: dziękuję.

PW: Wątpię w sens tak dokładnego wyznaczania dziedziny (ja wiem, w szkole tak uczą itd. ... ale cała para idzie w gwizdek i łatwo się pomylić). Praktycznie wystarczy napisać: − równanie ma sens dla takich x, dla których sinx > 0 i √2sinx≠1 i 1+cosx > 0 − dla takich x równanie jest równoważne (zgodnie z definicją logarytmu) równaniu (1) (√2sinx)² = 1 + cosx. Po rozwiązaniu (1) w R sprawdzić, które rozwiązania spełniają wszystkie trzy nierówności.

tyu: dzięki PW za zainteresowanie