wartosc bezwzgledna Blue: Rozwiąż nierówność: ||x|−3|<2 Rozwiązuje tak, jak jest tutajhttps://matematykaszkolna.pl/strona/1108.html , ale wychodzi mi x∊R , jak to liczyć?

Piotr 10: A na końcu robisz sumę zbiorów czy część wspólną ?

J: ... ⇔ − 2 < IxI − 3 < 2 ⇔ 1 < IxI < 5 ... i teraz rozwiązuj..

Blue: sumę, a powinnam część wspólną tak Ale dlaczego?

Piotr 10: I IxI − 3 I < 2 IxI − 3 < 2 i IxI − 3 > − 2 IxI < 5 i IxI > −1 Więc widzisz, w 1⁰ i 2⁰ x∉R 1 0 − I xI < 5 2⁰ IxI > − 1 . Tutaj x∊R

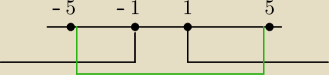
J: I teraz szukaj części wspólnej...

Blue: a to nie jest po prostu tak, że jak mam na początku ≤ to część wspólna, a jak mam ≥ to suma?

J: Bo muszą jednoczesnie byc spełnione dwa warunki: IxI < 5 i jednocześnie IxI > 1

Blue: zawsze jak mam podwójne wartości bezwzględne to jakoś tego wszystkiego nie potrafię sobie wyobrazić xd

J: Zielone ... IxI < 5 , czarne ...IxI > 1

J: Jeśli masz: IAI ≤ a , .... to część wspólna Jeśli masz : IAI ≥ a ,...... to suma przedziałów.

PW: Nierówność 1 < |x| < 5 proponuję po prostu "przetłumaczyć" z definicji modułu: − dla x ≥ 0 oznacza ona 1 < x < 5, − a dla x < 0 1 < − x < 5. Mamy więc do rozwiązania dwie proste nierówności na dwóch różnych kawałkach osi, rozwiązanie jest oczywście sumą tych dwóch rozwiązań

Blue: ok, dzięki za wytłumaczenie

pigor: ..., czyli analitycznie masz taki ciąg nierówności równoważnych: ||x|−3|<2 ⇔ −2<|x|−3<2 /+3 ⇔ 1<|x|<5 ⇔ |x|<5 i |x|>1 ⇔ ⇔ −5<x<5 i (x<−1 lub x>1) ⇔ (−5<x<5 i x<−1) lub (−5<x<5 i x>1) ⇔ ⇔ −5<x<−1 lub 1<x<5 ⇔ x∊(−5;−1) U (1;5) . ...