trygonometria tyu:

	2
mam ustalić ZW funkcji y=
	sin2x

tu jest wykres http://www.matemaks.pl/program-do-rysowania-wykresow-funkcji.php?funkcja=sin(x);sin(2x);2/sin(2x)&dokladnosc=200&skala=40.00&xc=-0.9&yc=1 ale nie wiem, dlaczego ta funkcja tak wygląda 1/ rysuję sobie y=sinx 2/ potem y=sin(2x) czyli każdy x mnożę przez k=0,5, zatem wykres jest dwa razy "ściśnięty" 3/ nie wiem jak wytłumaczyć to, że wykres tak "odbija" od osi OX na wysokości y=2 i y=−2 Wiem, że dla sinx ZW=<−1;1> i że 2 pomnożone przez krańce przedziału da (−2) oraz 2 albo może tak to się liczy

	2		2
y=		= −2 y=		= 2
	−1		1

no i na tym się kończy moja wiedza co do narysowanie tej funkcji.

tyu:

pigor: ..., no cóż ja bym robił tak :

	2		2		1		sin2x+cos2x
y=		=		=		=		=
	sin2x		2sinxcosx		sinxcosx		2sinxcosx

	sinx
=		+U(cosx}{sinx}=tgx+ctgxi sinx≠0 i cosx≠0,
	cosx

czyli masz sumę wartości punktów wykresu tangensoidy i cotangensoidy y=tgx+ctgx, gdzie x=2kπ i x=¹₂+2kπ , k=0,±1,±2,± ..., to równania asymptot pionowych w ten sposób mam zbiór wartości (−∞;−2>U<2;+∞).

tyu: dziękuję, Ja to przekształcałem od y=tgx+ ctgx

	π
Ale tgx i ctgx przecinają się w		czyli w 1 i (−1) więc skąd te 2 oraz (−2) ?
	4

o co chodzi z tymi asymptotami ?

Saizou : albo inaczej skończyć

	1		1
tgx+ctgx=tgx+		=a+		niech tgx=a
	tgx		a

	1
a+		≥2 dla a>0
	a

	1
a+		≤−2 dla a<0
	a

razor:

	2
y =
	sin2x

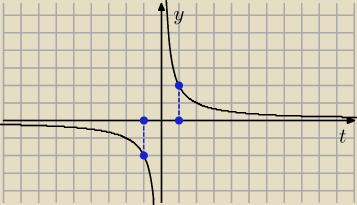
	2
podstawiam sin2x = t i t∊<−1,1> i badam zbiór wartości funkcji f(t) =		na przedziale
	t

<−1,1> Jak widać z wykresu ZW = (−∞, −2> ∪ <2, ∞)

tyu:

	π
asymptota ctgx to x=kπ, natomiast tgx to		+kπ
	2

tyu: dziękuję Wam wszystkim, ale wyjaśnienie, które przedstawił razor jest najbardziej łopatologiczne i dzięki temu już wiem, jak to narysować

pigor: ... , tam nie ma 1 i (−1) tylko jest (1 i 1) lub (−1 i−1), czyli np tg45^o+ctg45^o= 1+1=2 ... lub ... tg 135^o+ctg135^o= −1+(−1)= −2 ... itp. itd. dla k∊C . −−−−−−−−−−−−−−−−−−− a kończąc, to pięknie odczytał dziedzinę (wykorzystał znaną nierówność) Saizou