może ktoś mi pomoże jak takie zadania się rozwiązuje
michał: wyznacz wszystkie wartości parametru α α ∊ ≤ 0 , π ≥ dla których
sinα * x2 − sin 2α * x + 12 cosα = 0 ma dwa rozwiązania
wynik to α ∊ ( π2 , π )
2 sie 09:07
Piotr 10: A masz jakiś pomysł ?
Warunki trzeba ustalić.
2 sie 09:26
Kacper: Z jakim równaniem mamy do czynienia?
2 sie 11:13
Janek191:
sin α ≠ 0 ⇒ α ∊ ( 0 ; π )
Δ = ( − sin 2α)2 − 4*sin α * 0,5 cos α = sin2 2α − sin2α > 0
sin 2α *( sin 2α − 1) > 0 ⇒ sin 2α < 0
π < 2α < 2π / : 2
π2 < α < π
α ∊ ( π2 ; π )
===============
2 sie 16:43
michał: ale co z drugim nawiasem tzn ( sin2α − 1 ) dziękuję ale podobne zadanie to
wyznacz wszystkie wartości parametru α , α ∊ ≤ 0,π ≥ dla ktorych rozwiązania
cosα * x2 −2sinα *x + cosα są dodatnie
ja rozwiązałem to tak
cosα ≠ 0 ⇒ α ∊ ( 0, π), 0 < Δ = 4 sin2α − 4 cos2α = 4 sin2α −4 + 4 sin2α=5 sin2α − 4
dalej to nie wiem sugerowałem się przykładem powyższym
wynik ma być α ∊ ( π4, π2 )
2 sie 17:22
michał: ale może to jest poprawne
cosα ≠ π2
0 < Δ = 4 sin2α − 4 cos2α = 4 − 4 cos2α − 4 cos2α = 4 − 8 cos 2α
cos2α = 48 ⇒ cos α = √22 ⇒ x = π4 + 2kπ
czyli α ∊ ( π4,π2)
może ktoś sprawdzi czy to jest poprawne
2 sie 17:44
michał: jeszcze jedno mam zadanie z którym mam problem
sin4x − cos4x = 6m − cos22x ma co najmniej jedno rozwiązanie
wynik to m ∊ ≤ − 124 , 13 ≥
2 sie 21:19
Mila:
sin
4x − cos
4x = 6m − cos
2(2x) ma co najmniej jedno rozwiązanie.
Przekształcamy:
(sin
2x−cos
2x)*(sin
2x+cos
2x)+cos
2(2x)=6m⇔
(−cos(2x))*1+cos
2(2x)=6m⇔
cos
2(2x)−cos(2x)=6m
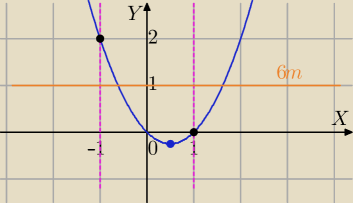
Ustalamy zbiór wartości funkcji
f(x)=cos
2(2x)−cos(2x)
cos(2x)=t i −1≤t≤1
f(t)=t
2−t
| | 1 | | 1 | |
f( |
| )=− |
| wartość najmniejsza f(t) |
| | 2 | | 4 | |
f(1)=1−1=0
f(−1)=1+1=2
=================
2 sie 21:39
Mila:
2)
wyznacz wszystkie wartości parametru α , α ∊ ≤ 0,π ≥ dla ktorych rozwiązania
cosα * x
2 −2sinα *x + cosα=0 są dodatnie
Δ=4sin
2α−4*cos
2α=−4cos(2α)
Δ≥0 aby istniały rozwiązania ⇔
−4cos(2α)≥0⇔cos(2α)≤0⇔
dla k=0
dla k=1 katy α nie należą do przedziału <0,π>
Wzory Viete'a
x
1+x
2>0 i x
1*x
2>0
| | c | |
i x1*x2= |
| =1>0 dla każdego α |
| | a | |
| 2 | | π | | 3π | |
| >0 dla cosα>0⇔x∊<0,U}{π}{2}) i α∊< |
| , |
| >⇔ |
| cosα | | 4 | | 4 | |
2 sie 22:08
michał: z jakiego wzoru powstał zapis Δ = 4sin2α − 4 cos2α = 4cos(2α)
2 sie 22:46
PW: Zgubiłeś minusik:
4(sin2α − cos2α) = −4(cos2α − sin2α) = −4cos2α
2 sie 22:51
Mila:
Witaj
PW 
2 sie 23:02
PW: Uszanowania

, coś wieje nudą, chyba pora spać.
2 sie 23:09
Mila:
Matematyka dyskretna.
Ile jest liczb stucyfrowych o sumie cyfr równej 4.
2 sie 23:23
michał: już wiem z jakiego wzoru, przepraszam że jestem dociekliwy
2 sie 23:38
michał: rzeczywiście zgubiłem minus dziękuję i dobranoc
2 sie 23:40
Mila:
Dobranoc, zawsze trzeba pytać, gdy są niejasności.

2 sie 23:45
michał: jeszcze raz powracam do zadania 2. tam korzystając ze wzoru Viete"a zamiast
x1+ x2 = 2cosα powinno być x1 + x2 = 2sinαcosα czyli 0< 2tgα
3 sie 13:05
Janek191:
sin 2α − 1 < 0 ⇒ sin 2α < 1 ⇒ 2α ≠ π2 ⇒ α ≠ π4
3 sie 13:35
michał: jeszcze jedno pytanie dla Janka 191 dlaczego jest zmiana znaku nierówności z większego na
mniejszy
3 sie 13:45
Janek191:
Δ > 0 ⇔ sin 2α *( sin 2α − 1) > 0 ⇔
⇔ [ sin 2α > 0 i sin 2α − 1 > 0 ] ⋁ [sin 2α < 0 i sin 2α − 1 < 0]
sin 2α > 0 i sin 2α > 1 − sprzeczność, bo sin 2α ≤ 1
Pozostaje
sin 2α < 0 i sin 2α < 1
============
3 sie 14:08
michał: podziękowania dla Janka191
3 sie 15:36
Mila:
Zadanie (2)
cosα * x2 −2sinα *x + cosα=0
Rzeczywiście w (2) trzeba uzupełnić i poprawić błąd.
wtedy mamy równanie :
−2sinα*x=0 i x>0 (z zał.)
x=0 nie są spełnione warunki
| | π | |
Δ=4sin2α−4cos2α=−4*(cos2α−sin2α)=−4cos(2α) i α∊<0,π>/{ |
| } |
| | 2 | |
⇔
| | π | | π | | π | | 3π | |
α∊< |
| , |
| )∪( |
| , |
| > |
| | 4 | | 2 | | 2 | | 4 | |
3)
Dobrze napisałeś x
1+x
2 =2tgα
x
1*x
2=1 niezależnie od wartości α
odp.
W zadaniu nie jest podane, że rozwiązania mają być różne, dlatego dałam Δ≥0
To jest ciągle problem budzący wątpliwości.
Jeśli jest sformułowanie
dwa różne rozwiązania dodatnie to warunek:
Δ>0 i odpowiedź
Chyba już nie ma pomyłek.
3 sie 17:59
michał: dziękuję
3 sie 18:57
 sin4x − cos4x = 6m − cos2(2x) ma co najmniej jedno rozwiązanie.
Przekształcamy:
(sin2x−cos2x)*(sin2x+cos2x)+cos2(2x)=6m⇔
(−cos(2x))*1+cos2(2x)=6m⇔
cos2(2x)−cos(2x)=6m
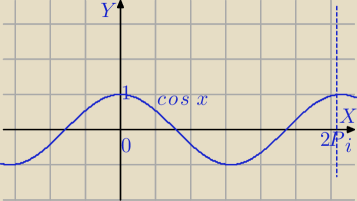
Ustalamy zbiór wartości funkcji
f(x)=cos2(2x)−cos(2x)
cos(2x)=t i −1≤t≤1
f(t)=t2−t
sin4x − cos4x = 6m − cos2(2x) ma co najmniej jedno rozwiązanie.
Przekształcamy:
(sin2x−cos2x)*(sin2x+cos2x)+cos2(2x)=6m⇔
(−cos(2x))*1+cos2(2x)=6m⇔
cos2(2x)−cos(2x)=6m
Ustalamy zbiór wartości funkcji
f(x)=cos2(2x)−cos(2x)
cos(2x)=t i −1≤t≤1
f(t)=t2−t
 2)
wyznacz wszystkie wartości parametru α , α ∊ ≤ 0,π ≥ dla ktorych rozwiązania
cosα * x2 −2sinα *x + cosα=0 są dodatnie
Δ=4sin2α−4*cos2α=−4cos(2α)
Δ≥0 aby istniały rozwiązania ⇔
−4cos(2α)≥0⇔cos(2α)≤0⇔
2)
wyznacz wszystkie wartości parametru α , α ∊ ≤ 0,π ≥ dla ktorych rozwiązania
cosα * x2 −2sinα *x + cosα=0 są dodatnie
Δ=4sin2α−4*cos2α=−4cos(2α)
Δ≥0 aby istniały rozwiązania ⇔
−4cos(2α)≥0⇔cos(2α)≤0⇔

 , coś wieje nudą, chyba pora spać.
, coś wieje nudą, chyba pora spać.
