planimetria Blue: Wykaż, że środkowa poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego ma długość równą połowie długości przeciwprostokątnej tego trójkąta. Można by tam prostokąt dorysować, ale nie wiem, jak to dalej napisać, żeby było udowodnione ... Pomożecie?

J: Zauważ,że środkowa jest promieniem okręgu opisanego na tym trójkącie ... i wnioski.

Blue: no ale jak mam te wnioski zapisać? Bo to logiczne, że musi wtedy ta środkowa być równa promieniowi , który jest równy połowie przeciwprostokątnej, ale jak to zapisać, żeby było "udowodnione"?

J: Zrób rysunek...narysuj środkową i pokaż,że środkowa jest połową przeciwprostokątnej .... przeciwprostokatna = 2r , środkowa = r

J: W komentarzu napisz ... przeciwprostokątna jest średnicą okręgu opisanego na tym trójkącie

Blue: i to wystarczy

J: Tak ... środkowa = r , przeciwprostokątna = 2r , czyli środkowa jest połową przeciwprostokątnej cnw

PW: Środek S przeciwprostokątnej AB jest środkiem okręgu opisanego na trójkącie (fakt powszechnie znany). Wierzchołek C kąta prostego należy do okręgu opisanego. Wniosek: SC ma długość równą promieniowi. Najważniejsze jest wprowadzenie oznaczeń, bo inaczej trudno zapisać nawet oczywiste spostrzeżenie.

J: Dlatego sugerowałem .... rysunek ...

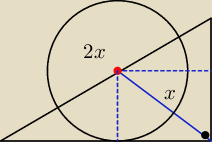
Hugo: z samego twierdzenia o stycznych do okręgu można

PW: Hugo, jeden z nas ma słaby dzień, bo nie rozumiem.

J: To teraz pokaż koleżance, jak to wykazać....., a Ona wybierze sobie sposób.

Blue: dzięki za pomoc

Hugo: nie wiem czy samym pitagorasem by sie nie dało

Blue: Dla mnie ten sposób z okręgiem jest chyba najlepszy (bo najprostszy, heh)

Hugo: PW Z twierdzenia wiemy że Hugo nie myli się nigdy a o co chodzi

J: "Hugo" ... nie wyważa się otwartych drzwi..., tego się trzymaj.

Hugo: moc Hugusia bazuje na HUG−SACH !

PW: A tak w ogóle to pierwsza myśl najlepsza, [PNBlue]]. Trójkąt prostokątny jest połową prostokąta. O prostokącie wiemy, że − jego przekątne połowią się (jak w każdym równoległoboku) − mają równe długości. Wniosek: środkowa o której mówi zadanie, ma długość równą połowie przekątnej prostokąta, czyli połowie długości przeciwprostokątnej.

Blue: o tym mówiłam na początku

Hugo: PW no w końcu

Hugo: Blue Berry która klasa ?

PW: I słusznie. Widzę, że zawzięłaś się nauczyć przeprowadzania dowodów. Uważaj, bo to wciąga i jeszcze zostaniesz matematyczką.

Hugo: PW − Patron Woodstock'u?