trygonometria tyu: zadanie z tych banalnych, ale mam problem

	1
cos3x <
	2

	π
czyli cos3x <
	3

	π
cosx3x =		⇒
	3

	−π		π
3x=		+ 2kπ lub		+2kπ
	3		3

więc

	−π		2kπ		π		2kπ
x=		+		lub		+
	9		3		9		3

odpowiedź to

	π		2kπ		5π		2kπ
x∊(		+		;		+		)
	9		3		9		3

	5π		2kπ
skąd się tam wzięło		+		wiem, że tu okres podstawowy jest 3 razy
	9		3

ściśnięty, ale nie potrafię tego wyliczyć ani narysować

Ajtek: W jakim przedziale to trzeba rozwiązać?

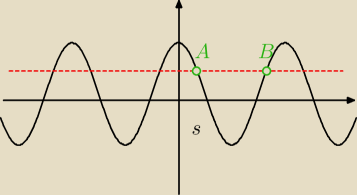
pigor: ..., cos3x< ¹₂ czyli cos3x< ^π₃ no nie, tak nie wolno napisać a ze swojego wykresu y=cost, t=3x odczytujesz nie alternatywę (lub), tylko koniunkcję(i), np. taką : ^π₃+2kπ < 3x < ^3π₂+^π₆+2kπ /:3 ⇔ ⇔ ^π₉+²₃kπ < x < ^9π₁₈+^π₁₈+²₃kπ ⇔ ⇔ ^π₉+²₃kπ < x < ^10π₁₈+²₃kπ ⇔ ⇔ x∊(^π₉+²₃kπ; ^5π₉+²₃kπ) .

Ajtek: I sprawa jasna, cześć pigor .

tyu: przedział nie jest określony tak, to ma być koniunkcja dziękuję za pomoc, ale mam kilka pytań

	3π		π
jak powstała prawa cześć nierówności 3x <		+		+ 2kπ
	2		6

	1		3π		π
wiem, że wykres jest poniżej y=		za liczbą		ale skąd te
	2		2		6

tyu:

tyu: ktoś pomoże , bo nie ruszę dalej.

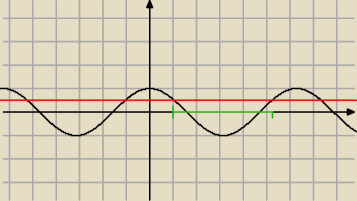Kacper: Na początek rozwiąż nierówność cosx<¹₂ Potem tylko przeskaluj na 3x (zaznaczyłem ci jeden przedział, powtarza się co okres)

tyu: WIEM. dziękuję