Geometria Blue: Kąty AOC i COB są przyległe. Narysowano dwusieczne k i l tych kątów oraz prostą równoległą do prostej AB, która przecina dwusieczne k i l odpowiednio w punktach D i E, a ramię OC w punkcie F. Udowodnij, że |DF|= |EF| Rysunek do zadania: http://i60.tinypic.com/8z0jf4.jpg

Blue: te kąty jakby co, to ja zaznaczałam

J: Δ FEO jest równiramienny i IFEI = IFOI Δ ODF jest równoramienny i IFOI = IDFI ... czyli IFEI = IDFI cnw

Blue: Nie wiem, czy takie udowodnienie wystarczy, ale podejrzewam, że nie, no bo skoro te trójkąty są równoramienne ( kąty naprzemianległe) , ale nie wiem, co tutaj jeszcze napisać...

Kacper: Własny pomysł jakiś?

Blue: czyli tylko to wystarczy

Blue: Kacper napisałam wyżej

Kacper: To jest w pełni poprawne wytłumaczenie. Dlaczego są równoramienne sama napisałaś

J: Czy widzisz ,że te trójkaty są równoramienne ? ... jesli tak, to : FE = FO = DF

Blue: J no widzę, bo przecież tam są kąty naprzemianległe nie? Ja wiem, ale tak się po prostu zastanawiałam, jak to napisać, bo z rysunku już można wywnioskować, jak się kąty zaznaczy

Kacper: Ale warto napisać

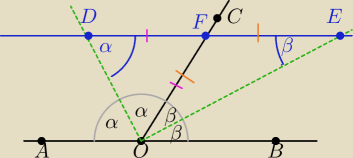
Mila: DE||AB ∡AOD≡∡FDO jako kąty naprzemianległe wewnętrzne ⇔ ΔDOF− Δrównoramienny,⇔ (1) |DF|=|OF| ∡BOE≡∡OEF jako kąty naprzemianległe wewnętrzne ⇔ ΔOEC− Δrównoramienny⇔ (2) |FE|=|OF| Z (1) i (2)⇒|DF|=|FE| cnw

Eta: Można też tak: trójkąt DOE jest prostokątny (α+β)=90^o Można na nim opisać okrąg to: |DF|=FC|=|OC|=r c.n.u

Kacper: |FC|=|OC|? z którego rysunku ?