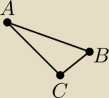
Jak obliczyć najprościej współrzędne punktu C tomker: Jak obliczyć najprościej współrzędne punktu C w trójkącie prostokątnym mając: Współrzędne: A (0,4) B (4,2) Długość odcinków AC=4,2 AB=4,5 Czy mogę prosić o rozpisanie tego przykładu?

Saizou : wiesz ze to zadanko ma nieskończenie wiele rozwiązań

tomker: Nawet mając takie dane?

Saizou : ale długość odcinka lABl =2√5 no i nie wiesz gdzie jest kąt prosty

tomker: kąt prosty jest w punkcie C

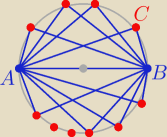
Eta: Takich trójkątów jest nieskończenie wiele Punkty C leżą na okręgu o średnicy |AB|

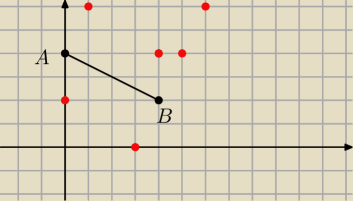
Saizou : czerwone kropki to tylko możliwe miejsca punktu C, no chyba że jakoś jest określona długość odcinka AC lub BC

Saizou : no i Eta już wszystko rozwiała tomker następnym razem przepisz treść całego zadania

tomker: O kurcze!

Eta:

jakubs: wektor AB=[4,−2] |AB|=√16+4 |AB|=2√5≠4,5

jakubs: Jestem taki szybki...

tomker: To nie zadanie z podręcznika. Obliczam najkrótszą drogę do odcinka o współrzędnych GPS z punktu wyjściowego A. Najkrótsza droga leży na odcinku powiedzmy KB i jest to punkt C

Saizou : wiesz że trudno jest pomóc jak nie wiadomo o co chodzi

tomker: Jest to zawiłe, ale przełożyłem to na taki przykład jak wyżej

Saizou : to napisz o co ci chodzi, bo inaczej będzie cięzko

tomker: żona mnie wzywa do łóżka, więc opiszę to dokładniej rano

Saizou : miłej nocy

Metis: "miłej"

Saizou: jak zona wola to trzeba isc i noc bedzie mila, bo z ukochana

Metis:

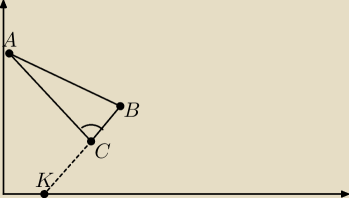
tomker: Czyli jeszcze raz. Jak obliczyć NAJPROŚCIEJ współrzędne punktu C w trójkącie prostokątnym mając DANE: Współrzędne: A (0,5) B (4,3) K (1,0) Długość odcinków: AC = 4,2 AB = 4,5 KB = 4,3 Kąt prosty jest w punkcie C Czy mogę prosić o rozpisanie tego przykładu?

razor: 1) Wyznaczyć prostą przechodzącą przez punkty K,B 2) Wyznaczyć prostą prostopadłą do niej przechodzącą przez punkt A 3) Z układu równań dwóch prostych wyliczyć gdzie się przecinają i otrzymać punkt C

?: ?

tomker: Pytam wielkiego brata Googla, o wzór na znalezienie punktu przecięcia się dwóch prostych prostopadłych mając dane takie jak w moim przykładzie, ale błądzę. Musi być jakiś jeden sensowny wzór. Po prostu potrzebuję to potem zaimplementować w programie komputerowym.

J: Nie ma uniwersalnego wzoru .... po prostu rozwiązujesz układ dwóch równań liniowych: A₁x + B₁y + C₁ = 0 A₂x + B₂y + C₂ = 0 .... równania prostych.

Kacper: Da się z tego zrobić jeden wzór ale nie będzie on zbytnio prosty

razor: Da się i nawet jakiś wstępnie wyprowadziłem ale już widzę że nie działa gdy punkty są na linii równoległej do którejś osi

Kacper: Trzeba dać rozgraniczenie na przypadki

tomker: Może być kilka wzorów, ale niech to będą wzory z wiadomymi, po w programie komputerowym nie mogę napisać z niewiadowmymi np. 3x

razor: A możesz dać układ równań do rozwiązania? Bo można by wyznacznikami wyliczyć x i y ale to jeszcze bardziej komplikuje rozwiązanie

tomker: Nie mam układu równań, tylko te dane, które wcześniej przedstawiłem. Czy da się w takim razie określić jedną wspł. punktu C (np. x) podstawiając znane nam wartości, a potem podstawić wynik do drugiego wzoru, który da nam wspł. y. Nie jestem matematykiem, więc trudno mi to ogarnąć.

5-latek: To sie z tym nie pie...l Podjedz na jakas uczelnie i zapytaj sie jakiegos Pana doktora jak to zrobic i po sprawie

daras: w końcu jest pełna treść i jak się domyślałem tylko JEDNO rozwiazanie a nie ∞

Saizou : daras a ja postuluję że nie ma rozwiązania, bo lABl=2√5, a nie 4,5

daras: @5−latek on ma tutaj swoich doktorów i się ich zapytowywuje nawet przez sen a swoje sprawy w tym czasie robi wiec po co ma marnowac czas na dojazdy

daras: @Saizou to nie było skorygowane od samego poczatku ale tryb pilny został włączony i doktory zaczęły w nocy rozwiazywac te ∞ ilości żeby śpioch miał gotowe jak się obudzi

daras: nic tu po mnie do Warszawy będziecie mieli kilka dni odpoczynku ode mnie

daras: i ja od was

tomker: Ale rozważania na mój temat. Wierzcie mi lub nie, ale głowię się nad tym od rana i zacząłem sam robić na podstawie tego co mi zaproponował @razor. Czyli ustalam równanie prostej jednej a potem drugą i będę próbował to jakoś w kodzie programu napisać. Widzę, że innego rozwiązania nie ma.

tomker: A tak, noc miałem przyjemną i nawet lepiej się myśli rano, jak kobieta przez całą noc cię przytula

Saizou : ja nadal nie rozumiem tego zadania, masz tam konflikt długości z współrzędnymi punktów (albo na odwrót możesz sobie wybrać)

tomker: Rozrysowałem sobie to na kartce i mierzyłem linijką, aby te dane były jak najbardziej przybliżone. Dlatego te długości podane w cm nie są na tip top, ale chodziło mi generalnie o podanie mi sposobu postępowania w obliczeniu, mając takie właśnie dane.

daras: jak się człowiek wyśpi, to się lepiej myśli

MQ: Najprościej liczy się to rachunkiem wektorowym: 1. Liczysz rzut wektora BA^→ na wektor BK^→ 2. Punkt C to końcówka rzutu zaczepiona w p. B.

tomker: @MQ podałeś mi we wcześniejszym wątku sposób rozwiązania na znalezienie najkrótszego odcinka z punktu do odcinka. @Gotowiec podał mi też wzór na jeden z wariantów. Kontynuuje temat i muszę teraz poznać współrzędne tego punktu C, ale nie da się chyba obliczyć punkt C (rys z 8:16) poprzez rzut, bo niby jak?

MQ: Da się −− korzystam z przykładu 8:16 BA^→=[−4,2] BK^→=[−3,−3] Rzut:

	[−4,2]◯[−3,−3]		12−6		1
W→=		*[−3,−3]=		[−3,−3]=		[−3,−3]=[−1,−1]
	[−3,−3]◯[−3,−3]		9+9		3

C=B+W^→=(4,3)+[−1,−1]=(3,2)

tomker: Mogę jeszcze obliczyć z twierdzenia Pitagorasa długość odcinka BC, ale czy to mi coś da? Próbowałem to obliczyć za pomocą układu równań, ale oprogramować to w PHP jest ciężko, więc wole jakieś inne rozwiązanie, może nawet dłuższe, ale bez niewiadomych.

tomker: O rzesz ..

tomker: @MQ jesteś WIELKI Działa! Sprawdzałem na kilku przykładach. Obyś w życiu doznał tyle szczęścia, jakich ja teraz doznaję.

MQ: Wielcy to byli ludzie, którzy ten rachunek (wektorowy) stworzyli. Niemnej za życzenia dziękuję