Zadanko:) Blue: Udowodnij, że punkty przecięcia par dwusiecznych kątów wewnętrznych prostokąta , który nie jest kwadratem, są wierzchołkami kwadratu. Zrobiłam to zadanko, jednak nie jestem pewna, czy do końca wszystko poprawnie uzasadniłam Daję Wam link do mojego rozwiązania i bardzo proszę o opinię, czy to rozwiązanie jest poprawne Z góry dzięki za odp. http://pl.tinypic.com/view.php?pic=2zqtoxu&s=8#.U9gPaZrwGM8 (Przepraszam za gryzmoły)

kochanus_niepospolitus: Jak dla mnie trochę 'słabe' uzasadnienie równości długości boków kwadratu. Co do wykazania kątów prostych uwag nie mam

Kacper: Rzeczywiście twierdzisz np, że te trójkąty są równoramienne, a brakuje uzasadnienia

Kacper: Twój rysunek nie przedstawia także jedynej sytuacji możliwej w zadaniu

Blue: a jak powinnam te boki udowodnić?

Kacper: Popatrz na trójkąty ABG i DEC

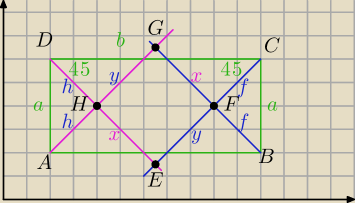
Mila: 1) EFGH jest prostokątem ( to wykazałaś) 2) ΔCBF≡ΔADH− jako Δrównoramienne prostokątne o przeciwprostokątnej a⇔h=f 2)ΔABG≡ΔDCE − jako Δrównoramienne prostokątne o przeciwprostokątnej b ⇒y+f=x+f⇔ y=x czworokąt EFGH jest kwadratem.

Blue: a więc to tak... no ale połowę pkt bym dostała xd

Kacper: Połowa to czasem za mało

5-latek: Wlasnie powtarazam liczby rzeczywiste . Mila w poscie 30.o7 1758 napisala ⇒y+f=x+f⇔y=x Na podstawie jakie prawa dzialan na liczbnach mozna tak napisac Blue?

J: Cześć "małolat" .. ... chodzi Ci chyba o twierdzenie, a nie prawo ?

Godzio: A to przypadkiem nie jest aksjomat ?

J: .... myślę o twierdzeniu o równaniach równoważnych , uzasadniającym równoważność tych dwóch równań: y + f = x + f ⇔ x = y

Kacper: W teorii grup było coś takiego jak prawo śkreśleń (redukcji) o ile dobrze pamiętam

5-latek: Witam Panow Prawo skreslenia :Jezeli ai b sa dowolnymi liczbami rzeczywistymi to : 1. dla dowolnego c a+c=b+c to a=b 2. dla c nie rowna sie 0 a*c=b*c to a=b Tak mam zapisane w ksiazce

Kacper: skreśleń

Kacper: Oczywiście dowodzi się tego faktu, ale nie na poziomie licealnym

J: Twierdzenie: Dla każdego c prawdziwa jest równoważność: a = b ⇔ a + c = b + c Z powyższego twierdzenia wynika, że do obu stron równania możemy dodać dowolną liczbę lub całe wyrażenie i otrzymamy równanie równoważne. Jeżeli od każdej ze stron równania odejmujemy liczbę, to korzystamy wówczas z tego samego twierdzenia (dodajemy liczbę przeciwną do obu stron równania).

5-latek: Kacper ja to mam zapisane w ksiazce do klasy 1 techniku i liceum zawodowego (1971r) A Ehrenfeucht i O Stande . Na razie sie z niej ucze bo powtarzam to za duze slowo teraz w moim przypadku

J: Twierdzenie to rozszerza się również na nierówności ... a ≥ b ⇔ a + c ≥ b + c

5-latek: J potem mam takie zadanie nr 21

	1		1
a) Co wiemy o x i y jezeli x+		=y+		Na podsztwie jakiego prawo tak twierdzisz ?
	3		3

	29		29
b) na podstawie jakie prawa twierdzisz ze jesli		x=		y to x=y
	17		17

Dlatego zapytalem

J: Ad a) ... na podstawie twierdzenia Ad b) .... na podstawie twierdzenia ....

J: Tak przy okazji .... co za archaiczne sformułowania zadań. Autor zadania jeszcze nie wie, co twierdzisz, a już pyta dlaczego tak twierdzisz ..

5-latek: J Spojrz tutaj pod koniec http://www.google.pl/url?sa=t&rct=j&q=&esrc=s&frm=1&source=web&cd=2&cad=rja&uact=8&ved=0CC0QFjAB&url=http%3A%2F%2Fpl.wikibooks.org%2Fwiki%2FMatematyka_dla_liceum%2FZaczynamy%2FDzia%25C5%2582ania_arytmetyczne&ei=riraU9uNHonZ4QTH_YDoAw&usg=AFQjCNG1cjIirHsPdHgOi3M19k2N4ksGMA

J: No cóż ... Wiki to autorytet , ale ja obstaje przy innej terminologii ...( nie uznaję w matematyce słowa: "skreślamy") .. ... skreślić można sudenta z listy...

5-latek: Jutro bede wstawial kolejne zadania wiec jeslli bedziesz mial ochote to i checi to mozesz mi pomoc