Równanie kwadratowe z wartością bezwzględną Yarek: Rozwiąż równanie | x² − 4x | = 6 − | x | Próbuję robić je już enty raz i nie wychodzi... Pierwsza wartość bezwzględna to funkcja kwadratowa, której ramiona skierowane są do góry, a miejscami zerowymi są 0 i 4, a więc przyjmuje wartości dodatnie (−∞;0)∪(4;∞), zaś ujemne (0;4). Druga wartość bezwzględna to jasne, x≥0. Zaczynając przedziały: 1' xε(−∞;0) − | x² − 4x | powinna być dodatnia, zaś | x | ujemna 2' xε<0;4) − | x² − 4x | powinna być ujemna, zaś | x | dodatnia 3' xε<4;∞) − | x² − 4x | powinna być dodatnia, zaś | x | dodatnia Rozwiązując te przedziały niestety nie dostaję takich samych pierwiastków, jakie są w odpowiedziach. Gdzie tkwi błąd? Proszę niezmiernie o pomoc i z góry dziękuję.

MQ: Wartości bezwzględne zawsze są ≥0, więc trochę mieszasz. Powinno być tak: 1': x²−4x=6+x 2': −x²+4x=6−x 3': x²−4x=6−x

Yarek: Suma sumarum tak otrzymałem, jak Ty napisałeś, ale wyszło mi źle... 1' x² − 4x − x − 6 = 0 x² − 5x − 6 = 0 △=25−24=1 x=2 v x=3 oba nie pasują do przedziału, a w tym przedziale powinna byc −1 W sumie 2' i 3' przedziały mam w porządku odpowiedzi, tylko w 1' jest źle.

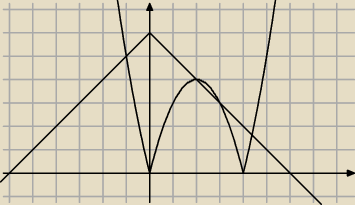
Kacper: |x²−4x|=6−|x| i rysunek i teraz odczytamy

MQ: Δ źle wyliczyłeś

Eta: Δ=25+24=.....

Yarek: Cholerka, dziękuję pięknie.