Przynajmniej jeden przykład. Proszę! Puaal: Zapisz zbiór w postaci sumy przedziałów a. R\(−5;4) B. R\<4,6> C. R\ (−3;−2> D. R\<1;4)

JP: 555555222≥∊∫→⇔

Puaal: Raczej nie o to mi chodizło.

Eta: a) (−∞, −5)U(−5, 4)U(4,∞) ( bo wyrzucasz −5 i 4 ze zb. R b) (−∞,4) U( 6,∞) bo wyrzucasz cały przedział <4,6> c) ( −∞, −3> U ( −2,∞) , bo wyrzucasz przedział z końcen −2 i bez początku −3

Puaal: dziękuję baardzo. Srasznie

Nikka: Eta a czemu −3 domknięty w c? w a przy −5 i zostawiłaś otwarty! jak dla mnie w c powinno być (−∞,−3)∪(2,∞)

Eta: Witaj Nikka Dzięki za zwrócenie uwagi w 1/ , potraktowałam ,że to zbiór dwuelementowy stąd mam sumę aż trzech przedziałów ( napisałam w wyjasnieniu) dopiero teraz widzę ,że to przedział obusrtonnie otwarty ( "ślepota" mnie napadła zatem do 1/ poprawka: ( −∞, −5> U <2,∞) bo te obydwa końce zostają .......... w c) na bank jest tak jak podałam

Nikka: ok, już rozumiem (należy do R, a nie należy do wyłączonego przedziału)

Puaal: Dzięki wielkie.A wie ktoś ja zrobić przykład d

Nikka: podobnie

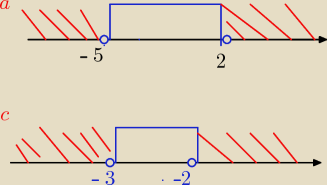
Eta: niebieski przedział ( −5, 2) −−− bez końców ,bo są poza nim czerwone przedziały to ta różnica i obydwa końce są w nich zatem R \ (−5,2)= (−∞, −5 > U < 2,∞) c) −3 została w czerwonym −2 poza czerwonym więc R \ (−3, 2> = ( −∞, −3> U ( −2,∞) to świetny sposób , podany przez Bogdana i od tej pory go stosuję nie używając : kółeczek, zamalowanych Polecam

Paula: Dobrze zrobione? D (−∞,1> u <4,∞)

Nikka: (−∞∞,1)∪<4,∞)

Paula: dzięki

Eta: Tak jak napisała Nikka 1 było więc wypadnie! 4 nie było , więc zostanie (−∞, 1) U < 4, ∞) idę coś