aa Hugo: wytłumaczcie mi coś: jak mamy zapis: lim_x→c+0f(x)=p to o co chodzi z tym c+0

Kacper: Skąd takiego stworka masz?

Hugo: Inne sposoby zapisu i wysłowienia granicy funkcji "zamiast mówić granicą funkcji f w punkcie c jest iczba g mówimy tez funkcja f dązy do g, gdy x dąży do c albo funkcja f ma granice g, gdy x dąży do c. zamiast limx→c+0 f(x)=p piszemy tez f(x)→_x→c+0p / ktos wie? to jest stara ksiażka moze tak bylo dawniej

zombi: x→ c+0 granica prawostronna w punkcie c

Mila: x dąży do stałej (c) z prawej strony.

zombi: Inaczej x dąży do c z prawej strony.

zombi: Mila

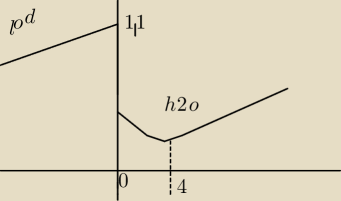
Hugo: 1. rozumiem że jak by bylo x→c−0 to z lewej strony 2.A jak mam takie coś: wykres rozszerzalności i zamarzanie wody, x− temperatura , f(x)−objętość w zależności od temp x i taki tam niżej: lim_x→0−0f(x)=1,1−0 i nie wiem co to znaczy ze x→0−0 a potem tam gdzieś dalej jest x→0+0 3.dziękuję !

Hugo: :((?

Hugo: .

zombi: 1. tak 2. x dąży do 0 z lewej strony/ x dąży do 0 z prawej strony 3. żaden problem.

Hugo: mam pytanie jeszcze zombi wracając do przykladu a) limx_→0−0f(x)=1,1−0 oraz b) limx_→0+0f(x)=2−0 W a) mamy odpowiednio 1,1−0 i 0−0 ( i jak mi wytłumaczyleś to granicą jest lewa strona)! a w b) mamy 2−0 oraz 0+0 i i jak mi wytłumaczyleś to granicą jest prawą strona jednak jak się przypatrzyłem w pierwszym mamy dwa znaki 'minus' a w drugim raz plus raz minus Czyli rozumieć mam że to tak ma być że w normalnej notacji po 'równa sie' zawsze jest 'minus' przyklad: ...f(x)=2−0 bądź f(x)=1,1−0 nie zależnie czy w prawo czy w lewo sie domyka, ważne jest to pod lim i to to decyduje

Hugo: .

Hugo: ktoś może mi doprecyzować ?

Hugo: 21:06 ktoś może mi to doprecyzować czy dobrze sądzę?

Kacper: Skąd masz takie zapisy z jakiej książki?

Hugo: ;___: nie wiem poczekam na zombiego albo Milę : > Kacper jesteś maturzystą? robisz coś do przodu?

Kacper: Jak nie wiesz musiałeś z jakiegoś źródła korzystać Zazwyczaj zapisujemy lim_{x → x0⁺} f(x) − granica prawostronna funkcji f w punkcie x₀ lim_{x → x0⁻} f(x) − granica lewostronna funkcji f w punkcie x₀ Ja już jestem "trochę" starszy

Hugo: jeszcze coś innego : O

Hugo: ale no dzięuję... bo to jest nie fajne że wiadomo o co chodzi a tyle możliwosci zapisu a dziekan i tak powie coś inneog

jakubs: Czemu dziekan ?

Hugo: wykładowca xd cicho

Kacper: Wykładowca może pełnić stanowisko prodziekana Czy dziekana to nie wiem

Mila: Hugo, skąd wytrzasnąłeś te zapisy?. Jest tak, jak pisze Kacper x→1₋ x→1₊ x→0₋ x→0₊ Rozwiązuj zadania z aktualnych polskich zbiorów zadań.

Maslanek: Zapis 0−0 oznacza, że od liczby 0 odejmujemy nieskończenie małą. Podobnie 0+0 oznacza, że do liczby 0 dodajemy nieskończenie małą.

Hugo: To by mialo sens bo wykres ilustruje funkcje objetosci lodu i wody w zaleznosci od temperatury − x , gdzie argumentem kluczowym funkcji f stanowiacym granice jest x=0 dziekuje ! Milo mam nadziedzieje ze wyjasnilem a motyw jest z ksiazki 'Zarys Matematyki Wyzszej' Roman Leitner cz.1 str 233

Maslanek: Ciekawostka taka, że liczba 0⁻ jest znowu nieskończenie dużą liczbą ujemną

Hugo: Maslanek: czyli mozn bylo by powiedziec ze x→0−0 jest rownowazne z tak jakbym X→0 −∞ Jako liczba 'nieskonczenie mala'

Maslanek: 0−∞=−∞ to dość logiczne Po odjęciu od czegoś małego czegoś dużego, dostaniesz coś dużego

Hugo: Albo jeszcze nowe przemyslenie x −> 0−0 od zera odejmujemy liczbe nieskonczenie mala t ak Czylize funkcja f zbliza sie do zera ale nigdy go nie osiaga ? F(x) nalezy (−oo ; 0) gdyz x−> 0−0 , a pozycje '0−0' odpowiadaja wartosci ( ,0) ?

Hugo: Maslanek jestes zombim i Mila moim nalepszym mentorem dziekuje

Maslanek: 0⁻, tudzież 0−0 to określenie lewej granicy zera. Czyli rzeczywiście czegoś bardzo bliskiego zera, ale będącego też "daleko", bo nigdy go nie osiąga

MQ: Widać po dylematach Hugona, że Hugo jeszcze nie zaczął studiów.

Mila: Stara się zrozumieć wstęp do matematyki.