nierownosc z wartoscia bezwzgledna
gad: nierownosc z wartoscia bezwzgledna : |x+3|=1−|3−x| rownanie ma byc sprzeczne , ale mi wychodzi
w przedziale (−3;3> wartosc x=1/2 dlaczego nie jest ona uwzgledniona w odpowiedziach?
26 lip 13:43
pigor: ... źle ci wychodzi i tyle np. narysuj wykresy L i P strony, to
nie mają punktów wspólnych; a co do x=12, to podstaw 0,5 równania
to zobaczysz, że nijak L−ewa strona nie równa P−rawej .
26 lip 14:52
Mila:
|x+3|=1−|3−x| ⇔
|x+3|=1−|x−3|
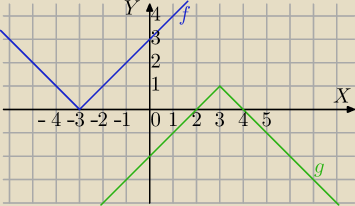
1) Najlepiej graficznie jak radzi
pigor.
f(x)=|x+3|
[Z[g(x)=1−|x−3|
2) metoda algebraiczna
a) |x+3|=x+3 dla x≥−3
b) |x−3|=x−3 dla x≥3
Rozważamy równanie w przedziałach:
1) x<−3 wtedy równanie ma postać:
−x−3=1−(−x+3)⇔−x−3=1+x−3
−2x=0⇔x=0∉(−
∞,−3)
2) x∊<−3,3)
x+3=1−(−x+3)⇔
x+3=1+x−3
3=−2 sprzeczność, brak rozwiązań w tym przedziale
3) x∊<3,
∞)
x+3=1−(x−3)
x+3=1−x+3
2x=1
Odp. Brak rozwiązań.
26 lip 20:40
gad: super dzieki mila wiem gdzie zrobilem blad nie wzilem pod uwage ze iks dla ostatniego
przedzialu niekoniczenie zawsze jest dodatni ale na ciebie zawsze mozna liczyc pozdrawiam
26 lip 22:39
pigor: ... a w pamięci : to
|x+3|=1−{3−x| ⇔ |x+3|+|x−3|=1 , a to geometrycznie : na prostej Ox
nie istnieją x których suma odległości od −3 i 3 równa się 1

26 lip 22:46
ICSP: |a| + |b| ≥ |a + b|
zatem
|x+3| = |x + 3| + |3 − x| − |3 − x| ≥ |x + 3 + 3 − x| − |3 − x| = 6 − |3 − x| > 1 − |3−x|
Równanie sprzeczne.
26 lip 22:48
Mila:
Niestety ta interpretacja jest zbyt trudna dla uczniów, często nieznana.
L=|x+3|+|3−x|≥|x+3+3−x|=6 najmniejsza wartość funkcji f(x)=|x+3|+|3−x|
26 lip 22:53
 |x+3|=1−|3−x| ⇔
|x+3|=1−|x−3|
1) Najlepiej graficznie jak radzi pigor.
f(x)=|x+3|
[Z[g(x)=1−|x−3|
2) metoda algebraiczna
a) |x+3|=x+3 dla x≥−3
b) |x−3|=x−3 dla x≥3
Rozważamy równanie w przedziałach:
1) x<−3 wtedy równanie ma postać:
−x−3=1−(−x+3)⇔−x−3=1+x−3
−2x=0⇔x=0∉(−∞,−3)
2) x∊<−3,3)
x+3=1−(−x+3)⇔
x+3=1+x−3
3=−2 sprzeczność, brak rozwiązań w tym przedziale
3) x∊<3,∞)
x+3=1−(x−3)
x+3=1−x+3
2x=1
|x+3|=1−|3−x| ⇔
|x+3|=1−|x−3|
1) Najlepiej graficznie jak radzi pigor.
f(x)=|x+3|
[Z[g(x)=1−|x−3|
2) metoda algebraiczna
a) |x+3|=x+3 dla x≥−3
b) |x−3|=x−3 dla x≥3
Rozważamy równanie w przedziałach:
1) x<−3 wtedy równanie ma postać:
−x−3=1−(−x+3)⇔−x−3=1+x−3
−2x=0⇔x=0∉(−∞,−3)
2) x∊<−3,3)
x+3=1−(−x+3)⇔
x+3=1+x−3
3=−2 sprzeczność, brak rozwiązań w tym przedziale
3) x∊<3,∞)
x+3=1−(x−3)
x+3=1−x+3
2x=1
