okrag hiperbola gad:

	4
Dany jest okrąg o środku w punkcie (1,1) i promieniu r oraz hiperbola y=		podaj ile
	x

punktow wspolnych maja okrag i hiperbola w zalenosci od r , prosze o pomoc

J:

	4
Równanie okręgu: (x−1)2 + (y−1)2 = r2, teraz podstaw za y: y =		i zbadaj ilość
	x

rozwiązań otrzymanego równania w zależności od parametru r

J: I założenenie: x ≠ 0

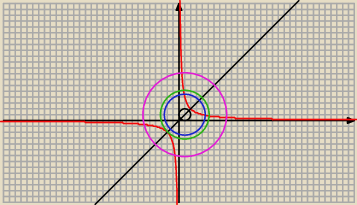
Janek191: S = (1; 1)

	4
y =		; x ≠ 0
	x

Prosta o równaniu y = x jest osią symetrii danej hiperboli Znajdujemy punkty wspólne prostej z hiperbolą :

	4
x =
	x

x² = 4 x = − 2 lub x = 2 y = − 2 lub y = 2 A = ( − 2; 2) B = ( 2 ; 2) Obliczamy odległości punktu S od punktów A i B : I AS I = √ ( 1 − (−2))² + ( 1 − (−2)² = 3√2 I BS I = √ ( 1 − 2)² + ( 1 − 2)² = √2 1) r < √2 − brak punktów wspólnych okręgu z hiperbolą 2) r = √2 − jeden punkt wspólny − B 3) √2 < r < 3√2 − dwa punkty wspólne 4) r = 3√2 − trzy punkty wspólne 5) r > 3√2 − cztery punkty wspólne

Janek191: Poprawka − miało być A = ( − 2; − 2)