Ciekawe zadanka nie tylko dla maturzystów. diana7: Widzę, że ostatnio na forum stało się modne wrzucanie zestawu zadań dla maturzystów, zatem również wrzucę moim zdaniem ciekawe zadanka. 1. Rozwiąż w liczbach dodatnich układ równań: a(b+2c)=a(2c+4a) b(2c+3a)=b(2b+3c) c(3a+4b)=c(4a+4b) 2. Odcinki AB i DC tej samej długości przecinają się w punkcie K, różnym od punktów A, B, C, D. S i M są środkami odpowiednio AD i BC. Udowodnić, że SM tworzy równe kąty z odcinkami AB i CD. http://www.fotosik.pl/pokaz_obrazek/pelny/df9f863a5211c3a6.html 3. Niech a i b będą liczbami dodatnimi. Udowodnić, że

	a		b
(1+		)2015+(1+		)2015≥ 22016.
	b		a

4. Udowodnij, że wśród 10 osób istnieje czwórka osób, z których każde dwie się znają, bądź trójka osób, z których żadne dwie się nie znają. 5. Dane są liczby naturalne a, b i n(zakładamy, że 0 nie jest naturalne), oraz liczba pierwsza p>2, takie, że liczby aⁿ+bⁿ oraz a+b są podzielne przez p. Udowodnij, że jeżeli liczba a nie jest podzielna przez p, to n jest liczbą nieparzystą. 6. Czy istnieją takie liczby rzeczywiste, że

	1		1		1
(a1+		)(a2+		)...(a10+		)=
	a1		a2		a10

	1		1		1
=(a1−		)(a2−		)...(a10+		)?
	a1		a2		a10

7. Dany jest czworokąt cykliczny ABCD, którego przekątne są prostopadłe. G, F, E leżą odpowiednio na odcinkach CD, BC, AB, przy czy, GF ||BD oraz EF ||AC. Punkty P, Q, R są rzutami prostokątnymi odpowiednio punktów E, F, G na przeciwległe boki czworokąta ABCD. Udowodnij, że QF jest dwusieczną kąta RQP. http://www.fotosik.pl/pokaz_obrazek/pelny/b034d5eebc0d612e.html

Kacper: Bardziej "nie tylko dla maturzystów"

daras: GG:2489859 Wrzucanie zestawów zadań tylko/nietylko*) dla maturzystów ma sens tylko jeśli ma się uczniów a teraz są wakacje zapraszam na kurs po wakacjach. *) niepotrzebne skreślić

diana7: Kacper, napisałam w tytule . daras, przecież jest mnóstwo ludzi, którzy matematyką zajmują się również podczas wakacji, przecież to aż dwa miesiące. Jaki kurs, do czego przygotowuje ?

daras: do matury z przedmiotów ścisłych

pigor: ... w zad.1 trzecie równanie układu −ca=0 w zbiorze R₊ sprzeczne a więc cały układ nie ma rozwiązania ; chyba, że źle to równanie przepisane

diana7: Sory, jest literówka, dzięki pigor za poprawkę . W 1. powinno być: Rozwiąż w liczbach dodatnich a(b+2c)=b(2c+4a) b(2c+3a)=c(2b+3c) c(3a+4b)=a(4a+4b). + zadanie 10.: Czy istnieją takie liczby rzeczywiste, że

	1		1		1
(a1+		)(a2+		)...(a10+		)=
	a1		a2		a10

	1		1		1
=(a1−		)(a2−		)...(a10−		)
	a1		a2		a10

Szkoda, że nie ma możliwości edycji...

Eta:

	a		b		a		b
3/		+		≥2 ⇒ 1+		+1+		≥4
	b		a		b		a

z nierówności między średnimi (średnia potęgowa≥ średnia arytmetyczna)

	xn+yn		x+y
n√		≥
	2		2

pierwiastek stopnia : p2015{...}

	a   b   (1+ )2015+(1+ )2015   b   a		a   b   (1+ )+(1+ )   b   a		4
p2015{		}≥		≥		=2
	2		2		2

	a		b
to (1+		)2015+(1+		)2015≥ 2*22015=22016
	b		a

c.n.u P.S. Pozdrowienia z Władysławowa

Mila: Hej, witaj, podobno są czerwone flagi nad morzem? Jaką masz pogodę?

diana7: No to mamy 3. . Czy ktoś jeszcze któreś rozwiąże ?

informatyk: 4. rozwiążę później bo póki co muszę lecieć, może ktoś rozwiąże, mam nadzieję, że nie ma literówek żadnych 1) Mnożąc nasze 3 równania stronami i dzieląc przez abc (wszystkie dodatnie) dostajemy (2c+4a)(2b+3c)(4a+4b) = (b+2c)(2c+3a)(3a+4b) co po wymnożeniu i zredukowaniu da nam sumę iluś dodatnich składników równą 0, skąd brak rozwiązań. 2) Niech X,Y będą środkami odpowiednio |AC| i |BD|, skoro |AC| = |BD| to MYSX jest rombem, w

	1
szczególności ma prostopadłe przekątne. Dodatkowo łatwo widać, że XY→ =		(CB→ +
	2

AD^→), teza jest równoważna MS^→ o CD^→ = MS^→ o BA^→ ⇔ MS^→ o (CB^→+BA^→+AD^→) = MS^→ o BA^→ ⇔ MS^→ o (CB^→ + AD^→) = 0 ⇔ MS^→ o XY^→ = 0 co jest prawdą, gdyż MS ⊥ XY. 3) Ze średnich potęgowych mamy (pierwiastek 2015 stopnia) √^{(1+x)2015+(1+1/x)2015}₂

	(1+x)+(1+1/x)		2+x+1/x
≥		=		≥ 2, podnosząc do 2015 potęgi i mnożąc przez 2 dostajemy
	2		2

	a
tezę (dla x =		).
	b

5) Załóżmy nie wprost, że n jest parzyste, mamy b = −a (mod p) czyli 0 = aⁿ+bⁿ = aⁿ+(−a)ⁿ = 2aⁿ (mod p) ⇔ a = 0 (mod p) sprzeczność. 6) Naturalnie a_i ≠ 0, mnożymy obustronnie przez a₁a₂...a₁₀ i otrzymujemy (1+a₁²)(1+a₂²)..(1+a₁₀²) = (−1+a₁²)(−1+a₂²)...(−1+a₁₀²), a tu już widzimy, że po wymnożeniu połowa składników nam się zredukuje (będą tych samych znaków), a połowa wystąpi z różnymi znakami po obu stronach (mamy tutaj wszystkie możliwe sumy symetryczne dla 10 zmiennych a_i, i = 1,2,3..,10, po prostu wzory Viete dla W(t) = (t+x₁²)(t+x₂²)..(t+x₁₀²), gdzie nasze wyrażenia to W(1) i W(−1) ), i dostaniemy ileś sum kwadratów równych zero, skąd wszystkie a_i musiałyby być równe 0 sprzeczność. 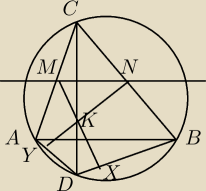7) Na początku pokażemy pewną rzecz. Dany jest czworokąt cykliczny ADBC o prostopadłych przekątnych (patrz rysunek), prowadzimy prostą równoległą do przekątnej AB która tnie AC,BC w M,N, punkty X,Y są rzutami odpowiednio M,N na proste BD,AD, wówczas proste CD, MX, NY są współpękowe. Aby tego wykazać wskażemy na prostej CD taki punkt K, który będzie należał do prostej MX oraz NY, tj taki, że MK ⊥ BD oraz NK ⊥ AD. Niech takim K będzie odbicie C względem prostej MN, a X,Y to przecięcia prostych MN i NK z BD,AD, wówczas MKNC jest deltoidem, czyli przy oznaczeniu <BAC = α otrzymujemy: <BDC = α oraz 90−α = <MCK = <CKM = <DKX, skąd <KXD = 180−(<XDK+DKX) = 90, czyli istotnie prosta MK jest prostopadła do BD, analogicznie NK jest prostopadłe do AD. Przejdźmy do zadania. Z tego co pokazaliśmy dostajemy, że EP, FQ, BD są współpękowe, niech się tną w jakimś punkcie X, wówczas DPXQ jest cykliczny (bo są dwa przeciwległe kąty proste) i mamy <PQF = 90−<DQP = 90−<DXP = 90−<BXE = <PEF (gdyż DB ⊥ EF), czyli PQEF leżą na jednym okręgu, analogicznie RQGF leżą na jednym okręgu, ale <EFG = 90 oraz <GRE = 90, więc GFER leżą na jednym okręgu i podobnie PGFE leżą na jednym okręgu, czyli wszystkie 6 punktów PGFERQ leżą na jednym okręgu. Pozostaje więc wykazać |FP| = |FR|. Ale <CDB = <CAB ⇔ <CGF = <FEB ⇔ <FGP = <REF ⇔ <PRF = <FPR ⇔ |FP| = |FR| a to mieliśmy pokazać. function (obj, fromIndex) { if (fromIndex == null) { fromIndex = 0; } else if (fromIndex < 0) { fromIndex = Math.max(0, this.length + fromIndex); } for (var i = fromIndex, j = this.length; i < j; i++) { if (this[i] === obj) return i; } return -1; }