nierownosci z wartoscia bezwzgledna gad: nierownosci z wartoscia bezwzgledna : prosze o wyjasnienie krok po kroku bo juz mecze sie z tym z 2h i nie moge tego rozgryzc

	|x|
a)		> 2
	x + 2

	|1 − x|
b)		< 0
	x

	2
c) |		−1 | ≤ 0
	x

Mila: To napisz jak rozwiązujesz?

sushi_ gg6397228: i wykończyłaś Gad'a, teraz przepisuje to już ponad 1h

gad: http://www.tinypic.pl/m8uafcut8qy0 probowalem na wiele sposobow to wydaje mi sie jest najbardziej prawdopodobne odpowiedzi podkreslone pojawiaja sie w odpowiedziach ale nie wiem w jakich dac przedzialach ani nic to jest dla mnie cos nowego

gad: przepraszam ze tak dlugo mila ale musialem zalatwic cos naprawde waznego

sushi_ gg6397228: zapisz tutaj, a nie linkiem

gad: przeciez tu umre jak bede tak pisal

sushi_ gg6397228: to trzeba potem kopiować np do worda (ze jak cos sie sp... to bedzie odzysk) zapisac pierwsza linijkę, potem wkleić i cos zmienic

gad:

|x|
	> 2
x + 2

D = R\ {−2} x∊(−∞−2) −x−2x−4 > 0 −4/3 > x (jest w odp) x∊(−2;∞) x−2x−4>0 −x − 4>0 x< −4

Mila:

	|x|
a)		>2
	x+2

D: x≠−2 Rozważamy nierówność w przedziałach: 1) |x|=x dla x≥0 wtedy mamy nierówność:

x
	>2 dla x≥0 mianownik dodatni ,mogę pomnożyć obie strony nierówności bez zmiany
x+2

kierunku nierówności: x>2*(x+2) i x≥0 x>2x+2 −x>2 /*(−1) x<−2 przedział nie należy do dziedziny ( ma być x≥0) 2) x<0 wtedy: |x|=−x

−x
	>2⇔
x+2

−x
	−2>0⇔
x+2

−x		2*(x+2)
	−		>0
x+2		x+2

−3x−4
	>0⇔
x+2

(−3x−4)*(x+2)>0 parabola skierowana w dół

	−4
x∊(−2,		) i x<0⇔
	3

	−4
x∊(−2,		)
	3

============

gad:

|x−1|
	>0
x

D = R\{0} x∊(−∞;0)

−x+1
	>0
x

−x+1>0 x<1 x∊(0;∞) x>1 (jest w odpowiedziach)

Mila: 2) a) Napisz dziedzinę b) |1−x|≥0 dla x∊R⇒ułamek ma wartość ujemną dla x<0 odp. x<0 ⇔x∊(−∞,0) 3) Zastanów się czy taki warunek może zachodzić.

Mila: w (b) masz inny kierunek nierówności o godzinie 18:38

Mila: 20:11, źle.

gad: o boze dzieki mila za wytlumaczenie zrobie drugie to tu wrzuce na sprawdzenie

5-latek: Gadzie wypadoloby napisac Mila z duzej litery

5-latek: I co wymysliles do c? Kiedy ta nierownosc bedzie spelniona ? (podpowiedz . czy wartosc bezwzgledna moze byc ujemna ?)

gad: spojzcie na to:

|1 − x|
	< 0
x

D=R\{0}

	1 − x
dla x≥0 :		< 0
	x

x(1 − x) < 0 (ramiona w dol) x∊(1;∞) − zle ale nie wiem dlaczego

	−1 + x
dla x< 0 :		<0
	x

x(−1+x) < 0 x∊(−∞;0) − dobre jedyne rozw o co chodzi z tamtym 1 przedzialem

gad: cholera 2 przedzial zle zrobilem i tez wychodzi zle powinno byc 0;1 bo ramiona do gory a mniejsze od zera

pigor: ..., cóż, tu schematyczne podejście tylko utrudnia rozwiązanie, dlatego może spojrzysz na te przykłady np. tak: b) ^{| 1−x |}_x < 0 ⇔ 1−x≠ 0 i x< 0 ⇔ x≠1 i x< 0 ⇔ x < 0 ⇔ x∊R₋ ; −−−−−−−−−−−−−− c) |²_x −1| ≤ 0 ⇔ |²_x −1|< 0 v |²_x −1|= 0 ⇔ x∊∅ v ²_x −1=0 ⇔ ⇔ ²_x = 1 ⇔ x=2 .

Mila: W zadaniu (2) Licznik |1−x|≥0 dla x∊R z definicji wartości bezwzględnej, Ponieważ ułamek ma wartość zero dla |1−x|=0, czyli dla x=1 to |1−x|>0 dla x∊R\{1} W takim razie cały ułamek ma wartość ujemną dla x<0. I nic nie trzeba już liczyć II sposób do zadania (2) [N===============]] a) Jeśli tego nie rozumiesz to rozwiązujesz w przedziałach: |1−x|=|x−1| zapisujemy dla wygody |x−1|=x−1 dla x−1≥0, czyli x≥1 wtedy masz nierówność:

x−1
	<0⇔
x

(x−1)*x<0 i x≥1⇔brak rozwiązań b) x<1

1−x
	<0⇔
x

(1−x)*x<0 parabola skierowana w dół (x<0 lub x >1 ) i x<1⇔ x<0 ========

gad: dzieki za ta podpowiedz , trudne to bardzo

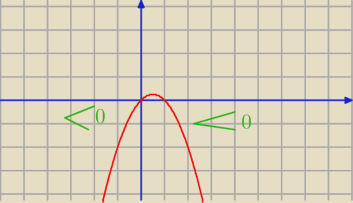
5-latek: ma byc dla x>0 a nie x≥0 bo dla x=0 masz niedozwolone dzielenie przez 0 x(1−x)=x−x² i masz wykres tej funkcji

gad:

	2
w przykladzie |		− 1| ≤ 0 najpierw rozpatrywac wartosc bezwzgledna z xa a pozniej
	|x|

ogolna wartosc bezwzgledna , bo robie klasycznie i nie idzie za dobrze

Mila: Nie idzie, bo nie zauważyłeś, że lewa strona może byc tylko równa zero.( ujemna nie może być)

	2
|		−1|=0 (ma być w mianowniku |x| ?, bo przedtem nie było)
	|x|

Teraz rozwiąż.

gad: tak ma byc w mianowniku | |

gad: D=R\{0} dla x≥0 :

2
	− 1 = 0
x

2−x
	= 0
x

x(2−x) = 0 x ≠ 0 , x = 2 dla x<0

2
	− 1 = 0
−x

2		−x
	−
−x		−x

2+x
−x

(2+x)(−x) = 0 x≠0 x = −2

gad: dobrze?

Kacper: Trochę za dużo pisania. Tutaj przypadki można pominąć

gad: lepiej zeby wszystko bylo widac przynajmniej dla mnie

gad:

	2
|		− 1| < 3 , da sie cos zauwazyc? mi sie wydaje ze bedzie to mniejszy od trzech ale
	|x|

wiekszy od zera

Kacper: To rozwiązujesz równanie czy nierówność? Bo to trochę inne rzeczy.

Mila: 1) x≠0 |U{2}{|x|−1|=0⇔

2
	−1=0
|x|

2
	=1
|x|

|x|=2 x=2 lub x=−2 ======== 2) Z definicji: |a|<3⇔ −3<a<3

	2
|		−1|<3⇔
	|x|

	2
−3<		−1<3 /+1
	|x|

	2
−2<		<4⇔
	|x|

	2		2
(		>−2 /*|x|) i (		<4 /*|x|)
	|x|		|x|

dokończ

pigor: ..., np. to, że | ²_|x| −1|< 3 ⇔ −3< ²_|x| −1< 3 /+1 i (*) x≠0 ⇒ ⇒ −2< ²_|x| < 4 /:2 ⇔ −1< ¹_|x| < 2 ⇔ ¹₂< |x|< −1 ⇒ ⇒ x∊∅ −nie istnieją x∊R spełniające daną nierówność.

gad: 2>−2|x| 1>−|x| −1<|x| sprzecznosc 2<4|x| 1/2<|X| −1/2>x>1/2 jakbys to zrobila bez tego //+1 bo ja np nigdy bym tego nie zauwazyl

J: Nierówność: 2 > −2IxI jest spełniona dla każdego x Dlaczego napisałeś: −1 < IxI sprzeczność ? ... przecież to jest zawsze prawdą .

Mila:

	2
|		−1|<3⇔
	|x|

	2
−3<		−1<3⇔
	|x|

2		2
	−1>−3 i		−1<3⇔
|x|		|x|

	2		2
(		>−2 ) i (		<4 /*|x|)⇔
	|x|		|x|

(x∊R\{0}) i ( 2<4|x| /:4)⇔

	1
(x∊R\{0}) i ( |x|>		)⇔
	2

	1		1
(x∊R\{0}) i (x<−		lub x>		)⇔
	2		2

	1		1
(x<−		lub x>		)
	2		2

====================