Bryły Blue: Podstawą ostrosłupa jest trojkat rownoboczny o boku dlugosci 4. Dwie sciany boczne tego ostorslupa sa prostopadle do plaszczyzny podstawy a trzecia tworzy z plaszczyzna podstawy kat o mierze 60 stopni. oblicz objetosc i pole calkowite ostroslupa. Objętość mi dobrze wyszła: 8√3, ale pole powierzchni mi wyszło 8√10+12+4√3, co jest źle, na pewno źle liczę te pola ścian bocznych ... mógłby ktoś jakoś to objaśnić, może narysować? Z góry dzięki za odp.

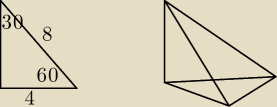
o nie: Piękny ? wychodzą krawędzie 4 przy podstawie, 8 na pochylonej płaszczyźnie i 4√3 na prostopadłej do podstawy. Pc to trójkąty (4,4,4),(4,8,8) i 2* (4,8,4√3), można liczyć wzorem herona, jest spoko wbrew pozorom

	1		1		1
V to		Pp*h czyli		*42√3*		*4√3 czyli 8?
	3		3		4

Blue: w odpowiedziach objętość jest podana taka, jak mi wyszła

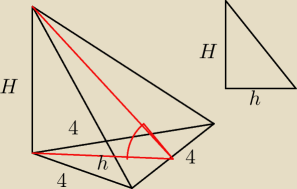
Kacper: h=2√3

	H
tg60=
	h

√3*2√3=H H=6

	1		1
V=		Pp*H=		*4√36=8√3
	3		3

Kacper: Teraz pole Na pole składają się dwie identyczne ściany każda ma pole 12, razem 24. Podstawa ma pole 4√3. Zostaje ostatnia ściana. Liczymy wysokość tej ściany.

	h		h		2√3
cos60=		⇒hb=		=		=4√3
	hb		cos60		12

Pole wynosi:

	1
P=		*4*4√3=8√3
	2

Ostatecznie: P_c=24+12√3=12(2+√3)

o nie: przepraszam, przyjąłem ten kąt w kompletnie złym miejscu i bardzo zamieszałem

Blue: Kacper a więc to tak wygląda − ja myślałam, ze wysokość ostrosłupa to jednocześnie wysokość tej jednej ze ścian bocznych... Dzięki za pomoc

Kacper: To tak jakbyś wycięła kawałek rogu pokoju