ddd sss: Triki matematyczne. Jakie znacie ?

Maslanek: 1+1=2. Przydatne

asdf: (a−b)² = (b−a)² fajne nie?

Eta: (a+b)²=(−a−b)²

Eta: 1*9+2= 11 (dwie jedynki) 12*9+3=111 123*9+4=1111 1234*9+5=11111 12345*9+6=111111 ................... 123456789*9+10=dziesięć jedynek

ae: Mnożenie liczb przez 100001.

Eta: np: 315*100001=31500315

Piotr 10: Fajny jest trik w liczach zespolonych: √3+4i = ? z = √3+4i z = x +yi x +yi = √3+4i (.. ) ² x² + 2xyi − y² = 3 + 4 i 1⁰ x² − y² = 3 2⁰ 2xy = 4 I teraz zamiast tworzyć równania dwukwadratowe, podstawienie x za y itd i liczyć to nie wiadomo ile , tworzę 3 dodatkowe równanie prawdziwe: 3⁰ x² + y² = √3²+4² I teraz szybko wyznaczam sobie iksa x² − y² = 3 x² + y² = 5 2x² = 8 x²=4 itd..

asdf:

AS:

	a + b		a − b
a*b = (		)2 − (		)2
	2		2

pigor: ..., no to ... : trik, nie trik

	f(x)+f(−x)		f(x)−f(−x)
tylko prawda f(x)=		+
	2		2

pigor: ..., a tak naprawdę , to zapewne chodzi o sofizmaty matematyczne ...

Mila: Zgaduję: √3+4i=(2+i) lub √3+4i=−2−i spr. (2+i)²=4+4i−1=3+4i (−2−i)²=4+4i−1=3+4i

baca: 15² = {1*2 z dopisaniem 5²| = 225 25² = {2*3 z dopisanie, 5²} = 625 35² = {3*4 z dopisaniem 5²} = 1225 45² = {4*5 z dopisaniem 5²} = 2025 55² = {5*6 z dopisaniem 5²} = 3025 itd

baca: 101² = {100 + 1 z dopisaniem (01)²} = 10201 {(01)² = 01} 102² = {102 + 2 z dopisaniem (02)²} = 10404 103² = {103 + 3 z dopisanie, (03)²} = 10609 104² = {104 + 4 z dopisaniem (04)²} = 10816 ..... 113² = {113 + 13 z dopisaniem (13)²} = 126 + (1)69 = 12769 114² = {114 + 14 z dopisaniem (14)²} = 128 + (1)96 = 12996

baca: 99² = {99 − 1 z dopisaniem (01)²} = 9801 98² = {98 − 2 z dopisaniem (02)²} = 9604 97² = {97 − 3 z dopisaniem (03)²} = 9409 96² = {96 − 4 z dopisaniem (04)²} = 9216 95² = {95 − 5 z dopisaniem (05)²} = 9025 albo 9*10 z dopisaniem 5², czyli 9025 94² = {94 − 6 z dopisaniem (06)²} = 8836 ...... 87² = {87 − 13 z dopisaniem (13)²} = 74 z dopisaniem (1)69 = 7569

baca: To nie wszystko, jest jeszcze wiele innych takich ułatwień rachunkowych

Eta:

baca: 97 * 92 = {od 97 do 100 jest 3 i 92 − 3 = 89 albo od 92 do 100 jest 8 i 97 − 8 = 89, wynik zawsze jest ten sam} = 89 i dopisujemy 3*8 otrzymując 8924 87 * 94 = {87 − 06 = 81 albo 94 − 13 = 81 i dopisujemy 13*6} = 8178

diana7:

	1
x3+y3+z3−3xyz=		(x+y−z)((x−y)2+(y−z)2+(z−x)2)
	2

Gustlik: Ciąg arytmetyczny dany wzorem postaci a_n=an+b, wtedy r=a, np. dla ciągu a_n=3n+5 r=3, można szybko odczytać różnicę. Jest ona zawsze równa współczynnikowi kierunkowemu prostej y=ax+b, w której zawiera się wykres danego ciągu.

Gustlik: Wartość bezwzględna: |a−b|=|b−a|. Można w równaniach i nierównościach zamieniać wyrażenie typu |2−x|=|x−2|, bo o wiele prościej się rozwiązuje, gdy x stoi na początku, a nie na końcu.

Gustlik: Pierwiastkowanie liczb typu a±b√c

	√a+x		√a−x
√a±b√c=		±		, gdzie x=√a2−(b√c)2.
	√2		√2

Najpierw obliczamy x, a potem "właściwy" pierwiastek. Nie trzeba wymyślać i wyszukiwać liczb pasujących do wzoru skróconego mnożenia, żeby to obliczyć.

Gustlik: Geometryczna metoda rysowania wykresu funkcji liniowej nazywana przeze mnie "schodkową" omówiona tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41 .

Gustlik: Równanie okręgu postaci x²+y²+Ax+By+C=0: Współrzędne środka:

	A
a=−
	2

	B
b=−
	2

Promień r=√a²+b²−C, gdzie a²+b²−C>0

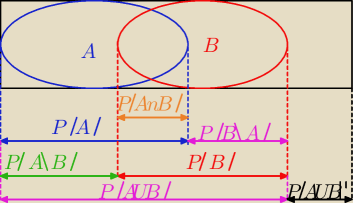
Gustlik: Graficzna metoda wykonywania działań na zbiorach i zdarzeniach oraz obliczania prawdopodobieństwa z jego własności, bez konieczności pamiętania wzorów. Nanosimy w odpowiednie miejsce wartości prawdopodobieństw podane w zadaniu, a resztę liczymy z rysunku, np. P(A\B)=P(A)−P(A∩B) itp. Należy pamiętać, że cały prostokąt to Ω, czyli jego prawdopodobieństwo, a więc długość = 1.

Gustlik: Obliczanie współczynnika kierunkowego prostej ze współrzędnych wektora leżącego lub równoległego do tej prostej:

	uy
u→[ux, uy] ⇒ a=		, gdy ux≠0.
	ux

Gdy u_x=0, mamy prostą pionową typu x=c. Ułatwia to wyznaczanie równania prostej przechodzącej przez 2 dane punkty A i B. Wyznaczamy współrzędne wektora AB^→=[x_B−x_A, y_B−y_A]=[u_x, u_y], to będzie ten nasz wektor u^→, a potem współczynnik kierunkowy wzorem jak powyżej. Obliczony współczynnik kierunkowy podstawiamy do równania prostej y=ax+b (np. jeżeli a=2, to mamy y=2x+b) i do tak wyznaczonego równania podstawiamy współrzędne jednego z punktów A lub B do wyboru − najlepiej wybrać te"wygodniejsze" do obliczeń, np. tam, gdzie nie ma ułamków albo liczb ujemnych itp. I liczymy b. Np: A=(3, 4) B=(5, 8) AB^→=[5−3, 8−4]=[2, 4]

	4
a=		=2
	2

Funkcja liniowa ma równanie y=2x+b Wstawiamy współrzędne np. A: 4=2*3+b 4=6+b b=−2 Równanie prostej y=2x−2

Gustlik: Obliczanie długości odcinka (odległości punktów) za pomocą wektorów: |u^→|=√u_x²+u_sup>2 Np. dla przykładu powyżej A=(3, 4), B=(5, 8): Najpierw liczymy współrzędne wektora AB^→ jak powyżej, a potem jego długość: |AB^→|=√2²+4²=√4+16=√20=2√5 Ta długość jest równocześnie długością odcinka AB i odległością tych punktów. I nie trzeba używać tasiemcowego i niezbyt wygodnego wzoru |AB|=√(x_B−x_A)²+(y_B−y_A)².

Gustlik: Obliczanie pól figur w układzie współrzędnych za pomocą wyznacznika wektorów omówione tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3423 .

Gustlik: Długość wektora |u^→|=√u_x²+u_y², coś musiałem źle wcisnąć.

Gustlik: Sprowadzanie funkcji homograficznej z postaci ogólnej do kanonicznej metodą dzielenia wielomianów: Np.

	2x+3
y=
	x−1

Ułamek to dzielenie, dzielę licznik przez mianownik jak wielomiany: 2 −−−−−−−−−−−−−−−−−− (2x+3):(x−1) −2x+2 −−−−−−−−−−−− 5 Resztę z dzielenia wpisuję nad dzielnik (czyli mianownik) i do tego dodaję wynik dzielenia:

	5
y=		+2
	x−1

I nie trzeba kombinować, co tu dodać sztucznie w liczniku, a potem odjąć, żeby rozbić na dwa ułamki i skrócić. To wyjdzie samo z dzielenia.

	5
Mam p=1, q=2, zatem mam funkcję y=		przesuniętą o wektor u→=[1, 2]
	x

Przypomina to wyłączanie całości z ułamków niewłaściwych:

	47		2
Np.		=9
	5		5

9 −−−−− 47 : 5 −45 −−−−−− 2

Gustlik:

	−b
"Bezdeltowy" sposób obliczania q w funkcji kwadratowej: q=f(p), gdzie p=		. Czasami jest
	2a

	−Δ
on szybszy od standardowego q=		. Obliczamy p, a potem wstawiamy wartość p za x do
	4a

wzoru funkcji. Jest to logiczne, ponieważ wierzchołek paraboli jest punktem lezącym na niej, a więc jego współrzędne, podobnie jak współrzędne kazdego punktu leżącego na paraboli muszą spełniać warunek wynikający z równania paraboli: (x, f(x)). Dla wierzchołka będzie to zatem (p, f(p)). Niestety ten sposób obliczania q na ogół nie jest pokazywany w szkołach, a jest bardzo przydatny, zwłaszcza przy obliczaniu współrzędnych wierzchołka niezupełnych funkcji kwadratowych typu f(x)ax²+bx, f(x)=ax²+c. Przydaje się on również przy sprowadzaniu funkcji z postaci iloczynowej do kanonicznej. Gdy znamy miejsca zerowe funkcji, to p mozemy obliczyć jako srednią arytmetyczną miejsc zerowych:

	x1+x2
p=		, bo wierzchołek leży "pośrodku" miejsc zerowych na osi symetrii,
	2

a q − sposobem "bezdeltowym" q=f(p) i mamy zadanie zrobione szybciej. Np. y=2(x−3)(x+5) Odczytujemy miejsca zerowe: x₁=3, x₂=−5

	3+(−5)
p=		=−1
	2

q=f(−1)=2*(−1−3)(−1+5)=2*(−4)*4=−32 Zatem wierzchołem paraboli W=(−1, −32), a postać kanoniczna y=a(x−p)²+q, czyli y=2(x+1)²−32.

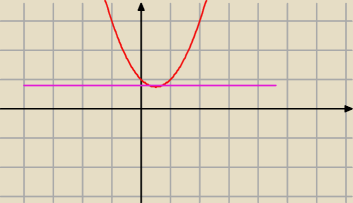
asdf: uzywajac pochodnych, proste wyprowadzenie argumentu p: gdy pochodna = 0 (kat nachylenia stycznej y = ax + b do osi OX), w tym miejscu jest wierzcholek: postac funkcji kwadratowej: f(x) = ax² + bx + c, gdzie a ≠ 0 (prosta definicja wielomianu 2 stopnia) f'(x) = 2ax² + b 2ax + b = 0 2ax = −b

	b
x = −
	2a

asdf: wyprowadzenie q:

	−b		−b		−b		ab2		b2
f(p) = f(		) = a*(		)2 + b*		+ c =		−		+ c =
	2a		2a		2a		4a2		2a

b2		b2		b2 − 2b2		−b2
	−		+ c =		+ c =		+ c
4a		2a		4a		4a

i proste wyprowadzenie: Δ = b² − 4ac −Δ = −b² + 4ac

−Δ		−b2
	=		+ c = q
4a		4a

chyba takich rzeczy nie pokazuja w LO, a powinni...

AS: Jak szybko sprawdzić poprawność mnożenia dwóch liczb? 25691 x 35702 −−−−−−−−−−− 917220082 Pierwsza część sprawdzania 25691 ; 2 + 5 + 6 + 9 + 1 = 23 ; 2 + 3 = 5 35702 ; 3 + 5 + 7 + 0 + 2 = 17 ; 1 + 7 = 8 5*8 = 40 ; 4 + 0 = 4 Druga część sprawdzania 917220082 ; 9 + 1 + 7 + 2 + 2 + 0 + 0 + 8 + 2 = 31 ; 3 + 1 = 4 Zgodność wyników w obu częściach. Metoda jest zawodna w przypadku popełnienia tzw. błędu czeskiego gdy np. w wyniku przestawi się dwie cyfry.zamiast 58 wstawi się 85

5-latek: To ze sie ani razu nie odezwal /a to oznacza ze wcale jej /ja to nie interesuje Poza tym niech sobie wpiszse w google triki matematyczne lub [Z[ciekawe triki matematyczne ]] i ma do wyboru do koloru

sss: Gustik sposób na działaniach i zbiorach przyda się, nie znałem tego. 5−latek wiesz nie miałem czasu przez pracę po za tym w internecie są w większości tylko sztuczki typu jak szybko mnożyć,dzilić itd.