.
Piotr 10: Liczby zespolone
x2+x + 1 = 0
Liczę sobie wyróźnik:
Δ = 1 − 4 = − 3
√Δ = +/ − √3i czy √Δ = + √3i ?
Bo w jednym z filmików spotkałem się, że 99% studentów piszę +√3i, a to podobno jest
niepoprawnie
Zaś w książce mam napisane, że i∊(0;1)
Zatem: Δ= 3i2 ⇒ √Δ=√3i
Która wersja jest prawdziwa i dlaczego ?
17 lip 19:39
Mila:
Równanie algebraiczne drugiego stopnia:
a*z
2 + b*z + c = 0,
o współczynnikach zespolonych rozwiązujemy w zwykły sposób, tzn. obliczamy wyróżnik
∆ = b
2 − 4ac i stosujemy wzory:
Zauważmy, że w tym przypadku (w przeciwieństwie do przypadku liczb rzeczywistych)
zawsze istnieje
√∆ — w istocie są dwa pierwiastki różniące się znakiem. Do powyższych
wzorów wystarczy podstawiać dowolny z nich (ten drugi da te same wartości z
1,2.
17 lip 19:58
WueR:
Podnies do kwadratu √3i oraz −√3i i zobacz czy dostaniesz −3 w obu przypadkach, czy nie.
17 lip 19:59
Piotr 10: Ja wiem, że to samo wyjdzie. Tylko oglądałem filmik na youtube i tak jedna osoba wspomniała o
tym.
To jak liczę pierwiastek z delty to ma być ona z minusem czy z plusem czy napisać +/ − ?
17 lip 20:02
WueR:
√Δ = {w∊C: w2=Δ} i tego bym sie trzymal. Wybrac mozna tylko jeden z elementow tego zbioru,
ale pamietajmy, ze jak napiszemy √−3 = {√3i}, to prawda to nie jest.
17 lip 20:02
Piotr 10: Określ geometrycznie zbiór punktów płaszczyzny zespolonej:
Iz − i I = Iz+2I
Hmm?
IaI=IbI
a=b v a=−b
to jedynie wiem
Jak to ruszyć ?
17 lip 20:42
Piotr 10: a może podstawienie z = x+yi ?
17 lip 20:53
Mila:
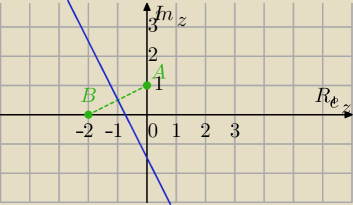
1) sposób,
|z−(0+i)|=|z−(−2+0i)| to jest równanie
symetralną odcinka AB, gdzie A=(0,1), B=(−2,0)
Napisz równanie symetralnej tego odcinka
2) sposób
Możesz tak ustalić zbiór punktów
z=x+yi
|x+yi−i|=|x+yi+2| ⇔
|x+i*(y−1)|=|(x+2)+y*i|
√x2+(y−1)2=
√(x+2)2+y2 /
2
x
2+y
2−2y+1=x
2+4x+4+y
2
−2y+1=4x+4
−2y=4x+3
17 lip 21:03
Piotr 10: 2 sposób łatwiejszy, mam pytanie do sposobu pierwszego
dlaczego tutaj jest symetralna odcinka AB ?
17 lip 21:14
Mila:
To z definicji.
Zbiór punktów jednakowo odległych od punktów (0,1),(−2,0)
17 lip 21:17
Piotr 10: To wynika z interpretacji geometrycznej

Szukam takich par liczb, których odległość pary (−2;0) od prostej jest równa odległości pary
(0;1) ?
17 lip 21:17
Mila:
Popatrz na 2 sposób, trzecia linijka oznacza , że odległość punktu P(x,y) od A(0,1) jest równa
jego odległości od punktu B(−2,0 ), a to jest zbiór punktów na symetralnej AB (geometria
analityczna kłania się).
17 lip 21:22
Piotr 10: Ok, dziękuję

17 lip 21:24
Godzio:
Co do delty warto zapisywać w ten sposób:
Δ = −3 = (
√3i)
2 (bez obliczania pierwiastka) i od razu
| | −1 + √3i | | −1 − √3i | |
z1 = |
| lub z2 = |
| |
| | 2 | | 2 | |
17 lip 21:38
Piotr 10: Oks

thx

17 lip 21:40
ae: Z jakiej książki korzystasz?
17 lip 21:45
Piotr 10: Podstawowe wiadomości teoretyczne i ćwiczenia dla studentów studiów inżynierskich H. Łubowicz,
B. Wieprzkowicz
17 lip 21:46
Piotr 10: a tak to jeszcze filmiki z youtube.pl
17 lip 21:48
Piotr 10: Rozwiąź równanie:
z
2 + IzI = 0
z
2 = IzI
2
IzI
2 + IzI = 0
IzI ( IzI+ 1 ) =0
z = 0 v IzI = − 1
Co robię źle ?

17 lip 22:08
Godzio:
z2 ≠ |z|
|z| to liczba rzeczywista, a z2 to zespolona.
17 lip 22:10
Godzio:
z = x + iy
|z| = √x2 + y2
17 lip 22:10
Godzio:
z
2 ≠ |z|
2 oczywiście

17 lip 22:11
Piotr 10: Ok. Dzięki
17 lip 22:13
Piotr 10: Witam.
z2 + IzI = 0
z= a+bi
IzI=√a2+b2
(a+bi)2 + √a2+b2 = 0
Jeśli ta suma ma być równa zero to.
(a+bi)2=0 i a2+b2 = 0
a2+2abi − b2 = 0
a2+b2=0
2a2+2abi=0
a(a+bi)=0
a=0 v a = −bi
b=0 v
Proszę o pomoc, będę później.
18 lip 10:50
Piotr 10: ?
18 lip 11:38
Mila:
(a+b*i)2+√a2+b2=0⇔
a2+2abi−b2+√a2+b2=0
(a2−b2+√a2+b2)+2ab*i=0
teraz do zera przyrównujesz część Re i część Im⇔
(a2−b2+√a2+b2)=0 i 2ab=0
Z drugiego : a=0 lub b=0⇒
dla a=0
−b2+√0+b2=0
√b2=b2
Rozwiązuj dalej sam
18 lip 15:32
Piotr 10: Ok. Mam dziękuję

18 lip 20:55
Mario: Piotr mozna zapytac z jakich podrecznikow uczysz sie tych liczb zespolonych ? Mialem plany
ogladac wyklady z PWr a potem robic zadania z Skoczylasa lecz nie moge nawet znalesc lekcji o
liczbach zespolonych na filmikach z PWr. Moze mnie ktos nakierowac ?
18 lip 21:15
18 lip 22:02
Piotr 10: Mario polecam etrapez liczby zespolone

. Masz tam 8 filmików, łącznie około 280 minut +
testy + ćwiczenia z odpowiedziami
18 lip 22:15
Mario: Ok dzieki

18 lip 22:17
18 lip 23:27
Piotr 10: Witam, natrafiłem na kolejny problem robiąc zadanie
Rozwiąź równanie:
I z − 1I+ ź = 3
Ix+iy − 1I + x − iy = 3
Jak to dalej ruszyć

19 lip 11:32
ICSP: |x + iy − 1| = |(x−1) + iy| = √(x−1)2 + y2
19 lip 17:26
pigor: ..., widzę to dalej tak :
z= x+yi= ? , gdzie
... ⇔
√(x−1)2+y2+x −yi = 3+0i ⇔
√(x−1)2+y2+x= 3 i −y=0 ⇔
⇔
√(x−1)2+y2= 3−x i 3−x ≥0 i
y=0 ⇒ |x−1|= 3−x i x≤ 3 ⇔
⇔ (x−1=3−x v x−1=x−3) i x≤ 3 ⇔ (2x=4 v x∊∅) i x≤ 3 ⇒
x=2,
zatem
z=2+0i=
2 − szukane
rozwiązanie danego równania. ...

19 lip 20:29
Piotr 10: Dzięki, zrobiłem, też mi wyszło z=2

19 lip 21:00
zorba:
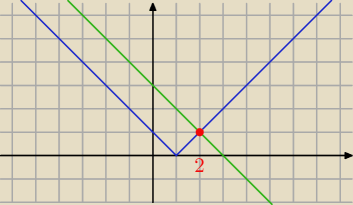 |z−1|
|z−1|=
3−z ,
z=2
19 lip 22:40
Piotr 10: Witam,
Oblicz:
3√(1+i)3
ω
0=1+i
| | 2π | | 2π | | 1 | | √3 | |
ω1 = ω0 * ( cos |
| + isin |
| ) = (1+ i ) * ( − |
| + |
| )= |
| | 3 | | 3 | | 2 | | 2 | |
| | 1 | | √3 | | 1 | | √3 | |
= − |
| − |
| + i(− |
| + |
| ) |
| | 2 | | 2 | | 2 | | 2 | |
ω
2 = .....
| | √3 | |
czy ω1 jest dobrze, bo w odpowiedzi jest inaczej jest plus przed |
| |
| | 2 | |
20 lip 18:26
Piotr 10: Ale tutaj nie muszę modułu liczby zespolonej liczyć, bo jeśli znam już jedno rozwiązanie to
korzystam ze wzoru
| | 2π | | 2π | |
ωk = ωk−1 * (cos |
| + isin |
| ) |
| | n | | n | |
20 lip 19:07
Janek191:
Piotr 10: Zgubiłeś i

przy obliczaniu ω
1
| | 1 | | √3 | |
= ( 1 + i)*( − |
| + i |
| ) = |
| | 2 | | 2 | |
20 lip 19:25
Mila:
W zapisie w pierwszej linijce zgubił "i", ale dobrze obliczył.
20 lip 20:03
Piotr 10: Witam,
Mam pewien problem w zrozumieniu postaci wykładniczej liczb zespolonych:
Przypuścmy, że mam taki przykład
( ź )
6 = 8zźIzI, gdzie ź to sprzężenie liczby zespolonej
z=IzIe
iφ = re
iφ , gdzie r ≥ 0
(re
iφ)
6 =8re
iφ *re
−iφr
r
6e
−6iφ = 8r
3*e
0
Porównuje:
r
6 = 8r
3
r=0 v r=2
I jak teraz przyrownać dalej ? Proszę o wytłumaczenie
I drugi problem jak z tej postaci:
Ir
3e
3φoiI opuścić moduł

21 lip 19:45
Piotr 10: Znaczy się na końcu w wykładniku mam błąd
I r3e3φi I
21 lip 19:53
Kacper: To mnie na studiach nie uczyli takich liczb zespolonych

i chyba dobrze, bo zastosowania nie
widzę

21 lip 20:14
Piotr 10: :(. A zastosowań to podobno mnóstwo ma

21 lip 20:49
Piotr 10: Pomoże ktoś i wytłumaczy problem ?

21 lip 21:06
mono:
Poproś
Milę 
21 lip 21:07
Piotr 10: Mila pomożesz

? Ja będę jutro.
21 lip 21:10
Mila:
Coś wymyślę.
Po co takie dziwadło rozwiązujesz?
21 lip 21:12
Mila:
Wskazówka :
Dwie liczby zespolone niezerowe są równe, gdy ich moduły są równe, a argumenty różnią się o
wielokrotność (2π)
W takim razie masz :
r
6*e
−6iφ = 8r
3*e
i0⇔
r
6=8r
3
−6φ=0+2kπ⇔
| | n*π | |
φ= |
| , n=0,1,2,3,4,5,6 |
| | 3 | |
Teraz liczysz
z
0=2*(cos0+i sin0)=2
.....
21 lip 22:00
Piotr 10: Ok dziękuję

22 lip 11:26
Piotr 10: Znajdź
Arg(1 − i ) , arg(1−i)
Czym to się różni ?
argument liczby zespolonej to kąt 'fi' φ
22 lip 13:42
Kacper: Zapewne błąd w druku

22 lip 13:54
Piotr 10: No właśnie na pewno nie

w odpowiedzi mam, że
Arg ( 1− i ) = U{7π}[4}
| | 7π | |
arg(1−i ) = |
| + 2kπ i k ∊ Z |
| | 4 | |
22 lip 13:56
ICSP: Arg − argument główny
arg − argument dowolny
22 lip 13:57
Piotr 10: Aaa ok to wszystko wyjaśnia, dzięki
ICSP 
22 lip 13:57
Kacper: Ja nigdy na to nie zwracałem uwagi

Ale po odpowiedzi widać, że oni tak oznaczają

22 lip 14:01
Kacper: ICSP wakacje?

22 lip 14:02
Piotr 10: Określ geometrycznie zbiór punktów spełniających waruneK:
Proszę o pomoc od czego zacząć

23 lip 18:50
Piotr 10: Prościejsze rzeczy umiem tego typu, np. arg ( z − i ) > U{π}[6} itd , Iz − i I + Iz +iI=8.
Ale w tym to nie wiem, próbowałem podstawienie, pomnożenie licznika i mianownika przez z − 1 i
też nic
23 lip 20:03
Mila:
Ten przykład zostaw.
Gdzie znalazłeś to zadanie?
24 lip 00:14
Piotr 10: Ok, więc widzę, że za trudne już robię dla mnie. Z książki ''Podstawowe wiadomości teoerytczne
i cwiczenia dla studentow inzynierskich''.
Mila jak będziesz to daj kilka zadanek( ze
trzy ) jak możesz z liczb zespolonych, bo właśnie kończę ten dział

24 lip 09:06
Kacper: np takie
narysuj na płaszczyźnie zespolonej zbiór punktów spełniających równanie
|z|+|z−1|=1

24 lip 09:55
Piotr 10: To będzie elipsa( tak na szybko) ?
24 lip 09:56
Kacper: pomyśl na powoli

24 lip 09:58
Piotr 10: To będzie półprosta ? y=0 i x ≥ 0 ?
24 lip 10:02
Kacper: to rozwiąż najpierw równanie
|x|+|x−1|=1

24 lip 10:14
Piotr 10: A po co ? źle ?
24 lip 10:17
Piotr 10: Ix+yiI+Ix − 1 +yiI = 1
√x2+y2 + √(x−1)2+y2 = 1
√(x−1)2+y2 = 1 − √x2+y2 ( .. )2
x2 − 2x+1+y2 = 1 − 2√x2+y2 + x2+y2
x = √x2+y2
x ≥ 0
y2=0
y= 0 i x ≥ 0
24 lip 10:31
Mila:
Dla sprawności rachunkowej.
1) |z|−z=1+2i
2) |z|+z=2+i
3) z*ź+z−ź=3+2i (4 rozwiązania)
4) i*(z+ź)+i(z−ź)=2i−3
24 lip 18:54
Piotr 10: Ok, dziękuję
Mila. A jak z tym zadaniem podanym przez
Kacpra 
?
24 lip 19:21
Piotr 10: 1)
IzI − z = 1+2i
√x2+y2 − x − yi = 1+ 2i
Przyrównuję teraz część rzeczywistą i część urojoną:
√x2+y2 − x = 1
−y=2 ⇒ y= − 2
Stąd:
√x2+y2 = 1+ x (..)2
Założenie: 1+x ≥ 0 ⇒ x ≥ −1
x2+y2 = (1+x)2
x2+4 = 1+2x+x2
2x = 3
x= 1,5 ∊ Zał.
Odp: z = 1,5 − 2i
24 lip 19:24
Piotr 10: 2)
√x2+y2 + x+yi = 2+i
√x2+y2 + x =2
y=1
√x2+y2 = 2 − x (..)
2
2−x ≥ 0 ⇒ x ≤ 2
x
2+y
2 = 4 − 4x + x
2
1= 4 − 4x
4x =3
24 lip 19:26
Kacper: Podstaw sobie liczbę 5 i sprawdź, czy jest dobrze

Szukaj błędu w twoich rachunkach

24 lip 19:35
Kacper: Te dwa oczywiście masz dobrze od
Mili 
24 lip 19:41
Piotr 10: No właśnie nie widzę błedu ( jak możesz to wskaż ).
3)
z*ź + z − ź = 3+ 2i
IzI
2+ x+yi − (x − yi) = 3+2i
x
2+y
2+2yi=3+2i
y=1
x=
√2 v x = −
√2
z=
√2 + i v z = −
√2 + i
Na pewno tutaj 4 rozwiązania

4)
i(z+ź) + i(z−ź)= 2i − 3
iz+iź +iz − iź = 2i−3
2iz = 2i−3
2xi − 2y=2i−3
2x=2 ⇒ x= 1
y= 1,5
z=1+U{3}[2}i
24 lip 20:02
Piotr 10: Tam na pewno w Twoim jest
IzI + I z −1I = 1 ?
24 lip 20:06
Kacper: tak na pewno

zobacz kiedy wolno nam podnosić do kwadratu obie strony równania

24 lip 20:26
Mila:
3) dobrze, źle odpisałam odpowiedź.
Teraz dać układy, czy równania kwadratowe?
24 lip 20:27
Piotr 10: Mila możesz dać jakieś trudniejsze troszkę. Równania kwadratowe to umiem chyba ( sama
delta prawie, chyba że jakieś trudne ).
Kacper
1 −
√x2+y2 ≥ 0
x
2+y
2 ≤ 1
O to chodzi ?
Ja będę później jak coś, bo wychodzę .

24 lip 20:31
Mila:
1) z3+1=0
2) z3−1=0
3)z3+i=0
24 lip 20:40
Piotr 10: 1)
z
3+1 = 0
z
3+1
3 = 0
(z+1)(z
2 − z + 1)=0
z+1=0 v z
2 −z +1=0
z = −1
z
2 − z + 1=0
Δ= 1 − 4 = −3
√Δ=
√−3 =
√−1*
√3=
√i2*
√3= I i I
√3 =
√3i lub −
√3i
| | 1+√3i | | 1 − √3i | |
z1= |
| v z2 = |
| |
| | 2 | | 2 | |
| | 1+√3i | | 1 − √3i | |
ODP: z = −1 v z = |
| v z= |
| |
| | 2 | | 2 | |
2)
z
3 − 1 = 0
(z−1)(z
2+z+1)=0
| | −1+√3i | | −1 −√3i | |
z= 1 v z= |
| v z2= |
| |
| | 2 | | 2 | |
3)
z
3+i=0
i
3= i
2*i= − i
i= − i
3
z
3 − i
3 = 0
(z−i)(z
2 +zi+i
2)=0
z= i
z
2+zi + i
2 = 0
z
2 + zi − 1=0
Δ = i
2 + 4 = −1+4=3
| | −i+√3 | | −i − √3 | |
z1= |
| v z2= |
| v z=i |
| | 2 | | 2 | |
Trzeba jeszcze najlepiej sprowadzić rozwiązania do postaci kartezjańskiej, czyli
| | −i+√3 | | √3 | | 1 | |
z1= |
| = |
| − |
| i .. itd  |
| | 2 | | 2 | | 2 | |
24 lip 22:25
Mila:
To jest postać kanoniczna.
Zaraz wpiszę następne.
IzI + I z −1I = 1 jaka do tego odpowiedź?
24 lip 23:01
Mila:
Zbiory punktów na płaszczyźnie zespolonej.
1) z*ź+(1+i)*z +(1−i)*ź=0
2) z*ź−(2−i)*z−(2+i)*ź=0
3) z*z−(3−4i)*z−(3−4i)*ź+2=0
24 lip 23:05
Mila:
cd.
5)|z−1|=|1+5i−z|
6) |z+2|+|z−2|=4
7) |z+2|+|z−2|=5
24 lip 23:13
Piotr 10: No właśnie nie wiem a propo tego zadania
IzI+ Iz−1I=1
y = 0 i x ≥ 0 i x2+y2 ≤ 1
?
24 lip 23:16
Mila:
IzI+ Iz−1I=1⇔
|z−0|+|z+1|=1
Zapis oznacza ,że suma odległości punktu P(a,b) od punktów A=(0,0) i B=(1,0) jest równa 1.
Punkty A i B są odległe od siebie o 1, zatem szukany zbiór punktów to odcinek AB.
Czyli tak , jak Ci wyszło:
y=0 i x≥0 i x≤1
W przypadku:
IzI+ Iz−1I=2 zbiorem punktów będzie elipsa, spróbuj znaleźć jej wzór, w razie kłopotów pomogę.
24 lip 23:46
Piotr 10: Mam coś takiego:
| | 3 | |
12x2+16y2 = 9 + 12x i x2+y2 ≤ 4 i x ≥ − |
| |
| | 2 | |
I coś mi tu nie gra, bo to chyba nie jest równanie elipsy:
| x2 | | y2 | | 9+12x | |
| + |
| = |
| |
| 16 | | 12 | | 192 | |
25 lip 10:13
Mila:
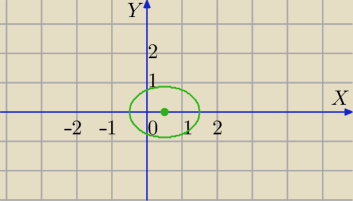
12x
2−12x+16y
2=9 /:12
25 lip 16:35
alim:
25 lip 16:43
Piotr 10: Ok, dziękuję. Nie wpadłbym na to, to przekształcenie. A te resztę zadań podanych przez Ciebie,
to raczej bym zrobił, ale nie chce mi się pisać

26 lip 09:33
Mila: /
28 wrz 15:38
 1) sposób,
|z−(0+i)|=|z−(−2+0i)| to jest równanie
symetralną odcinka AB, gdzie A=(0,1), B=(−2,0)
Napisz równanie symetralnej tego odcinka
2) sposób
Możesz tak ustalić zbiór punktów
z=x+yi
|x+yi−i|=|x+yi+2| ⇔
|x+i*(y−1)|=|(x+2)+y*i|
√x2+(y−1)2=√(x+2)2+y2 /2
x2+y2−2y+1=x2+4x+4+y2
−2y+1=4x+4
−2y=4x+3
1) sposób,
|z−(0+i)|=|z−(−2+0i)| to jest równanie
symetralną odcinka AB, gdzie A=(0,1), B=(−2,0)
Napisz równanie symetralnej tego odcinka
2) sposób
Możesz tak ustalić zbiór punktów
z=x+yi
|x+yi−i|=|x+yi+2| ⇔
|x+i*(y−1)|=|(x+2)+y*i|
√x2+(y−1)2=√(x+2)2+y2 /2
x2+y2−2y+1=x2+4x+4+y2
−2y+1=4x+4
−2y=4x+3
 Szukam takich par liczb, których odległość pary (−2;0) od prostej jest równa odległości pary
(0;1) ?
Szukam takich par liczb, których odległość pary (−2;0) od prostej jest równa odległości pary
(0;1) ?

 thx
thx 



 . Masz tam 8 filmików, łącznie około 280 minut +
testy + ćwiczenia z odpowiedziami
. Masz tam 8 filmików, łącznie około 280 minut +
testy + ćwiczenia z odpowiedziami




 |z−1|=3−z , z=2
|z−1|=3−z , z=2
 przy obliczaniu ω1
przy obliczaniu ω1

 i chyba dobrze, bo zastosowania nie
widzę
i chyba dobrze, bo zastosowania nie
widzę 



 ? Ja będę jutro.
? Ja będę jutro.


 w odpowiedzi mam, że
Arg ( 1− i ) = U{7π}[4}
w odpowiedzi mam, że
Arg ( 1− i ) = U{7π}[4}

 Ale po odpowiedzi widać, że oni tak oznaczają
Ale po odpowiedzi widać, że oni tak oznaczają 






 ?
?
 Szukaj błędu w twoich rachunkach
Szukaj błędu w twoich rachunkach 

 4)
i(z+ź) + i(z−ź)= 2i − 3
iz+iź +iz − iź = 2i−3
2iz = 2i−3
2xi − 2y=2i−3
2x=2 ⇒ x= 1
y= 1,5
z=1+U{3}[2}i
4)
i(z+ź) + i(z−ź)= 2i − 3
iz+iź +iz − iź = 2i−3
2iz = 2i−3
2xi − 2y=2i−3
2x=2 ⇒ x= 1
y= 1,5
z=1+U{3}[2}i
 zobacz kiedy wolno nam podnosić do kwadratu obie strony równania
zobacz kiedy wolno nam podnosić do kwadratu obie strony równania 


 12x2−12x+16y2=9 /:12
12x2−12x+16y2=9 /:12
