funkcja wymierna
Kondi: | | −2IxI−1 | |
pomoże mi ktoś narysować tą funkcje i wytłumaczyć jak to zrobił |
| |
| | IxI+2 | |
tzw wiem że bierzemy pierwsze bez zmian dla x>0 dzielimy i dostajemy asymptoty i dla x<0
analogicznie ale mi to nie wychodzi

17 lip 14:45
ICSP: | | −2|x| − 1 | | −2|x| + −4 + 4 − 1 | |
f(x) = |
| = |
| = |
| | |x| + 2 | | |x| + 2 | |
| | −2(|x| + 2) +3 | | 3 | |
= |
| = |
| − 2 |
| | |x| + 2 | | |x| + 2 | |
| | 3 | |
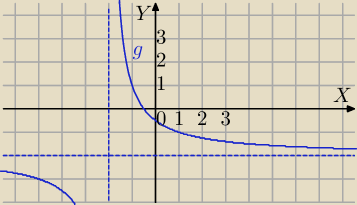
Rysujesz g(x) = |
| − 2. Potem zauważasz, że f(x) = g(|x|) |
| | x + 2 | |
17 lip 14:54
Mila:
17 lip 17:26
Mila:
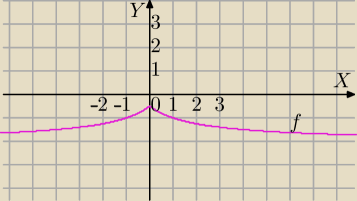
17 lip 17:29
Kondi: no tak ale skąd ta hiperbola przybrała taki dziwny kształt czemu nie widze asymptot pionowych i
czemu przecina oś y akurat w tym punkcie?
18 lip 22:08
Stępień:
| | 2x − 1 | | −2x − 1 | |
y = |
| y = |
| |
| | −x + 2 | | x + 2 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−−−−−−−−−−>
0
18 lip 22:15
Mila:
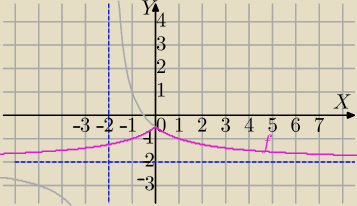
Widzę, że nie rozumiesz wykresu funkcji g(|x|).
17:26 masz wykres funkcji
Masz dwie asymptoty
x=−2 pionowa
y=−2 pozioma
wykres
| | 3 | |
f(x)=g(|x|)= |
| −2 powstaje z wykresu funkcji g(x) w taki sposób, że |
| | |x|+2 | |
Pomijamy wykres dla x<0, a odbijamy względem osi OY tę część wykresu z prawej strony osi OY.
(Dlatego, że |x|≥0, więc jeżeli podstawisz ujemny argument np. (−3)t |−3|=3)
Zostaje asymptoota pozioma y=−2.
Teraz powtórzę wykres z tą asymptotą.
18 lip 22:22
pigor: | | 2|x|+1 | |
..., funkcja f dana wzorem f(x)= − |
| jest parzystą f(−x)=f(x), |
| | |x|+2 | |
dlatego wystarczy narysować część wykresu funkcji f dla x≥o, a ponieważ
|−x|=|x|, to tak otrzymaną część odbij symetrycznie względem osi OY i tyle . ...

18 lip 22:56
Kondi: Aha... Dzięki wielkie naprawde całe dnie się nad tym głowiłem

19 lip 00:15



 Widzę, że nie rozumiesz wykresu funkcji g(|x|).
17:26 masz wykres funkcji
Widzę, że nie rozumiesz wykresu funkcji g(|x|).
17:26 masz wykres funkcji

