geometria (linie proste )
5-latek:
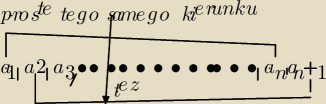
Przesledzic nastepujace rozumowanie .
NIech a
1 bedzie prosta . Oczywiscie a
1|| a
1
ROzwazmy dowolny uklad n+1 prostych a
1 a
2 a
3 ...... a
n, a
n+1 (n>=1 )
Jezeli kazde n prostych z tego ukladu nalezy do jednego kierunku to oczywiscie wszystkie n+1
prostych naleza do tego samego kierunku (patrz rysunek )
KOrzystajac z zasady indukcji udowodnilisny tym samym twierdzenie : Wszystkie proste
plaszczyzny sa rownolegle .
Znajdz blad w rozumowaniu . ( Mam do tego zadania wskazowke . Popelniono conajmniej dwa bledy )
17 lip 12:23
WueR:
Czy dowolny uklad n+1 prostych nalezacych do jednego kierunku to oby na pewno wszystkie proste
nalezace do plaszczyzny?
17 lip 12:34
WueR:
2. Zalozenie indukcyjne − n prostych nalezy do jednego kierunku. Wiec trzeba pokazac, ze n+1
prostych nalezy do tego samego kierunku. Ale rozwazamy dowolny uklad n+1 prostych, wiec czy
koniecznie (n+1)−sza prosta musimy dobrac tego samego kierunku?
17 lip 12:38
5-latek: Witam

ja mysle ze tak . Bo skoro a
1 nalezy do tego ukladu n+1 to wszyskie proste tego uklady tworza
plaszcyzne . jednak moge sie mylic
jesli cos wymyslisz (a napiszsez pozniej ) to zobacze okolo 23 jak wroe z przacy
17 lip 12:40
WueR:
n+1 calej plaszyczny raczej nie wygeneruje, bo to skonczona ilosc. Zeby wygenerowac cala
plaszczyzne, to oczywiscie wystarczyly by same proste rownolegle, ale musialo by ich byc
nieskonczenie wiele.
17 lip 12:56
5-latek: Tak masz racje (nie wzialem tego pod uwage ze to bedzie ilosc skonczona)
17 lip 12:57
WueR:
A ponadto tak jak wczesniej wspomnialem, sama indukcja jest blednie przeprowadzona. Warunek
pierwszy jest spelniony, bo a1||a1, pozniej zakladamy, ze n prostych nalezy do jednego
kierunku, wiec w drugim kroku musimy pokazac, ze n+1 prostych jest takich. W zalozeniu bylo,
ze rozwazamy dowolny uklad prostych, wiec ta (n+1) − sza prosta wcale nie musi byc tego samego
kierunku, co te n z zalozenia indukcyjnego.
17 lip 12:59
5-latek: A myslisz ze mozemy tutaj w tym przypadku stosowac twierdzenie o indukcji? (tak mi teraz
przyszsedl taki pomysl do glowy)
17 lip 13:01
WueR:
Hmm, w sumie nie wiem, czy ja cos nie pokrecilem teraz. Bo tam jest, ze dowolne n prostych z
tego ukladu jest tego samego kierunku. To by w sumie znaczylo, ze n+1 rowniez jest tego samego
kierunku.
17 lip 13:02
5-latek: Post 12:59 −Pewnie bedziesz mial racje .

Teraz muszse wyjechac do pracy (moze cos przy maszynie wymysle ) i dam znac co

17 lip 13:08
5-latek: WueR
Jeszc przed wyjazdem do pracy spojrzalem w inny zbior zadan i znalazlem rozwiazanie tego
zadania .
Piszsa tak : Popelniono dwa bledy :
1. przy przejsciu od n=1 do n=2 (prosta a1 nalezy do (a1 ) a2 nalezy do (a2) ale proste
a1 i a2 nie musza nalezec do tego samego kierunku. (wiec Ty miales racje )
2. Wiadomo ze prostych plaszczyzny nie mozna ponumerowac liczbami naturalnymi,d .latego tez nie
mozna stosowac twierdzenia o indukcji
jak sie na to zapatrujesz?
17 lip 23:08
WueR:
Co do 2. to wszystkich prostych o danym kierunku na pewno nie mozna ponumerowac, ja po
przeczytaniu tresci wyobrazilem sobie, ze po prostu wybieramy te n czy n+1 prostych z
wszystkich prostych o jednym kierunku. Stad moj post z 12:34 i uwaga (moze tam nie dosc
klarowna, bo to byla raczej wskazowka), ze jesli chcemy dowiesc czegos dla wszystkich
prostych, to rozwazamy wszystkie proste, a nie jakas ich czesc.
17 lip 23:17
5-latek: Na razie sobie odpuszcam rozwiazywanie zadan z geometrii.
Musze odpoczac i potem sie wziac za przeksztalcenia izometryczne. Powodzenia

17 lip 23:20
b.: Co do błedu nr 2 nie jestem przekonany:
wszystkie proste (z jakiegoś zbioru prostych) są równoległe oznacza − jak na mój gust − tyle,
że dowolne dwie proste (z tego zbioru) są równoległe. Równoległość jest relacją równoważności.
Liczność zbioru nie ma tu nic do rzeczy.
18 lip 01:08
5-latek: czesc b
W drugim bledzie chodzi o numeracje prostych(liczbami naturalnymi ) ,a nie ich ilosc
18 lip 14:21
Maslanek: Problem w błędzie nr 2 jest taki, że ilość prostych jest nieprzeliczalna (mocy continuum), zaś
zbiór liczb naturalnych jest przeliczalny (mocy alef 0)
Te dwa zbiory nie są równoliczne, więc nie można pokazać tej relacji równoważności (tutaj
zachowania kierunku, równoległości) poprzez zasadę indukcji matematycznej.
18 lip 16:13
daras: a czy 1 i 2 prosta z tego gatunku są do siebie ||

18 lip 16:47
b.: @5−latek, Maslanek:
No dobrze, to co to znaczy, że zbiór prostych, oznaczmy go przez A, jest zbiorem prostych
równoległych?
20 lip 22:25
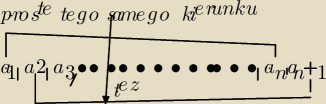 Przesledzic nastepujace rozumowanie .
NIech a1 bedzie prosta . Oczywiscie a1|| a1
ROzwazmy dowolny uklad n+1 prostych a1 a2 a3 ...... an, an+1 (n>=1 )
Jezeli kazde n prostych z tego ukladu nalezy do jednego kierunku to oczywiscie wszystkie n+1
prostych naleza do tego samego kierunku (patrz rysunek )
KOrzystajac z zasady indukcji udowodnilisny tym samym twierdzenie : Wszystkie proste
plaszczyzny sa rownolegle .
Znajdz blad w rozumowaniu . ( Mam do tego zadania wskazowke . Popelniono conajmniej dwa bledy )
Przesledzic nastepujace rozumowanie .
NIech a1 bedzie prosta . Oczywiscie a1|| a1
ROzwazmy dowolny uklad n+1 prostych a1 a2 a3 ...... an, an+1 (n>=1 )
Jezeli kazde n prostych z tego ukladu nalezy do jednego kierunku to oczywiscie wszystkie n+1
prostych naleza do tego samego kierunku (patrz rysunek )
KOrzystajac z zasady indukcji udowodnilisny tym samym twierdzenie : Wszystkie proste
plaszczyzny sa rownolegle .
Znajdz blad w rozumowaniu . ( Mam do tego zadania wskazowke . Popelniono conajmniej dwa bledy )
 ja mysle ze tak . Bo skoro a1 nalezy do tego ukladu n+1 to wszyskie proste tego uklady tworza
plaszcyzne . jednak moge sie mylic
jesli cos wymyslisz (a napiszsez pozniej ) to zobacze okolo 23 jak wroe z przacy
ja mysle ze tak . Bo skoro a1 nalezy do tego ukladu n+1 to wszyskie proste tego uklady tworza
plaszcyzne . jednak moge sie mylic
jesli cos wymyslisz (a napiszsez pozniej ) to zobacze okolo 23 jak wroe z przacy
 Teraz muszse wyjechac do pracy (moze cos przy maszynie wymysle ) i dam znac co
Teraz muszse wyjechac do pracy (moze cos przy maszynie wymysle ) i dam znac co 

