
 a)
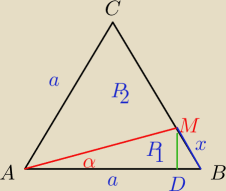
P1 = PΔAMB
P2 = PΔAMC
h2 − wysokość ΔAMB
x = I B M I
Mamy
P1 + P2 = P i P2 = 3 P1
więc
a)
P1 = PΔAMB
P2 = PΔAMC
h2 − wysokość ΔAMB
x = I B M I
Mamy
P1 + P2 = P i P2 = 3 P1
więc
| a2 √3 | ||
P1 + 3 P1 = | ||
| 4 |
| a2 √3 | ||
4 P1 = | ||
| 4 |
| a2 √3 | ||
P1 = | ||
| 16 |
| 3 a2 √3 | ||
P2 = | ||
| 16 |
| a2 √3 | ||
0,5 a*h2 = P1 = | ||
| 16 |
| a √3 | ||
h2 = | ||
| 8 |
| h2 | √3 | ||
= sin 60o = | |||
| x | 2 |
| a √3 | ||
x √3 = 2 h2 = 2* | / : √3 | |
| 8 |
| a | ||
x = I B M I = | ||
| 4 |
| a2 | 3 a2 | 4 a2 | 3 a2 | a2 | ||||||
y2 = x2 − h22 = | − | = | − | = | ||||||
| 16 | 64 | 64 | 64 | 64 |
| a | ||
y = | ||
| 8 |
| 7 | ||
z = I A D I = a − y = | a | |
| 8 |
| h2 | a √3 | 7a | √3 | |||||
tg α = | = | : | = | ≈ 0,2474 | ||||
| z | 8 | 8 | 7 |