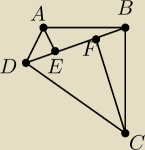
Ciekawa własność w pewnym czworokącie. mathb: W czworokącie ABCD kąty wewnętrzne przy wierzchołkach B i D są proste. Punkty E i F leżą na odcinku BD, przy czym odcinki AE i CF są prostopadłe do odcinka BD. Udowodnij, że DE=BF. Kto ma jakiś pomysł ?

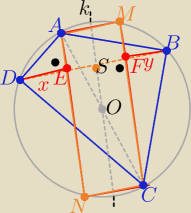
Eta: 1/Taki czworokąt można wpisać w okrąg, bo suma miar kątów D i B = 180^o 2/Prowadzimy prostą k zawierającą średnicę tego okręgu prosta k jest symetralną odcinka DB i jest równoległa do odcinków AE i CF 3/ przedłużamy AE i CF −−− otrzymujemy czworokąt AMNC, który jest prostokątem 4/ punkt S jest środkiem odcinka EF=2w , ES=w i SF=w 5/ punkt S jest też środkiem odcinka DB to: |DS|=|SB|⇒x+w=w+y⇒ x=y zatem |DE|=|FB| c.n.u

5-latek: Dobry wieczor Eta A mysmy mysleli ze jestes nad morzem i wypoczywasz

Eta: Witam Mila i 5−latek Właśnie wróciłam z brydża, a nad morze wybieram się w przyszłym tygodniu Myślę,że pogoda będzie tak ładna jak teraz

mathb: Dziękuję za rozwiązanie Eta .