Czworokąt wpisany w okrąg mathb: W czworokącie ABCD kąty CBA i CDA są proste oraz kąt BCD jest rozwarty. K jest odbiciem symetrycznym C względem AB, M jest odbiciem symetrycznym C względem AD, T jest przecięciem odcinków BA i KM. Udowodnić, że punkty C, T, A, M leżą na okręgu.

Metis: http://wstaw.org/m/2014/07/17/errete.png Wskaże ktoś mój błąd na rysunku ? Narysowałem czworokąt( wpisany w okrąg ) , zaznaczyłem kąt δ = CDA = 90 kąt β = CBA = 90 − kąty proste i kąt γ = BCD ≈ 115 − kąt rozwarty Odbiłem C względem AB, tak samo względem AD . Coś się nie zgadza.

mathb: Pomyliłeś punkt K z punktem M.

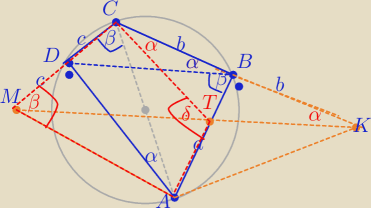
Mila: Szkic rozwiązania: Na czworokącie ABCD można opisać okrąg, suma miar kątów przeciwległych jest równa 180. Mamy wykazać, że suma miar kątów przeciwległych w czworokącie CTAM jest równa 180. ΔCMA, ΔCKA− Δrównoramienne DB jest odcinkiem lączącym środki boków ΔMKC⇔ DB|| MK β− katy wpisane w okrąg ,oparte na łuku AD ∡CMA=β − kąt przy podstawie ΔCMA, δ=α+90 jako kąt zewnętrzny ΔCBT α+β=90 − ΔCDA β+δ= β+α+90^o=90^o+90^o=180^o⇔ Na czworokącie CTMA można opisać okrąg. ============================= Jeśli masz pytania, to pisz.

mathb: Dziękuję za pomoc .

Mila:

Mila: Powinno być " na czworokącie CTAM".