Planimetria Blue: Działka budowlana ma kształt nieregularnego czworokąta. Wyniki pomiarów wykonanych przez geodetę są przedstawione na rysunku. Oblicz pole powierzchni tej działki. Podaj wynik przybliżony z dokładnością do 1m². Mógłby ktoś podpowiedzieć , jak podzielić ten czworokąt To nawet nie jest trapez, bo podstawy nie są równoległe. Nie mam pojęcia, jak to wyliczyć. Rysunek do zadania jest w linku poniżej (zad. 9) : http://pl.tinypic.com/view.php?pic=25i7swp&s=8#.U8PBM5rwGM8

jakubs:

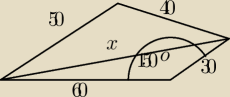
jakubs: Ja bym wyliczył x z tw. cosinusów i kąt między bokiem 50m i 40m, a następnie pola trójkątów z wzorku P=a*b*sina

jakubs: *między bokami 50m i 40m

Blue: Jakubs, ale to pierwsze jest chyba źle, bo te podstawy nie są równoległe i nie da się tego wyliczyć z własności trójkąta o kątach 90, 30, 60 ...

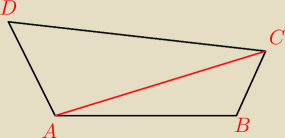
Soul Monster: Policz z tw.cosinusów prostą AC

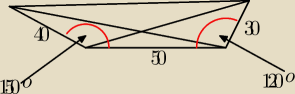
jakubs: Racja tamto źle.

	ef
Myślę nad wykorzystaniem wzorku P=		*sina, gdzie e,f−przekątne, a−kąt pomiędzy e i f.
	2

Zjem obiad to coś pomyślę dalej

Soul Monster: Policz z tw.cosinusów przekątną →wyznacz kąt pomiędzy przekątna a podstawą z tw.sinusów

Mila: To dobra propozycja. "Łatwiejszy" jest cosinus kąta.

K.: AC = 70, a ten kąt to mam w przybliżeniu podać?

Blue: Sorry nie zmieniła nicku, czasem podpisuje się też K. xD

Soul Monster: AC dobrze. Ułóż równanie z proporcji

a		b
	=
sinα		sinβ

Blue:

	3√3
wyszło mi sinα =
	14

Kacper: A nie masz odpowiedzi?

Soul Monster: Ok α=? Od kąta 150 odejmij α.

Blue: Kacper a co mi to da skoro w odpowiedzi mam tylko podane pole całej figury?

Blue: ok 22 stopnie?

Blue:

	1
a i teraz liczę pola tych dwóch trójkątów ze wzoru P =		absinα?
	2

Soul Monster: tak, teraz jak masz wszystkie kąty liczysz pole dwóch trójkątów, na końcu je sumujesz.

Mila: Kąt dobrze.

Blue: hmmm.... dziwne , bo mi wyszło, że P = 1478, 2, a w odpowiedziach mam , że ok. 1748.... To ja mam źle, czy w odp jest błąd

Mila:

1
	*(40*70*sin128+50*30*sin120)=
2

	1
=		*(2800*sin(52o)+1500*sin(60o))=
	2

= odczytaj 3 miejsca po przecinku dla sinusów

Blue: teraz mi wyszło 1752,7

Mila: Różnice wynikają z przyjętego przybliżenia wartości sinusów.

Blue: Czyli dobrze wyszło?

Mila: Myślę, że tak.

Blue: ok, dzięki wielkiee

Blue: a w tym drugim przykładzie jak wyliczyć kąt pomiędzy bokiem 50 i 40

Soul Monster: Najszybciej obliczyć przekątną dla β=150^o, później wyliczyć cosα.

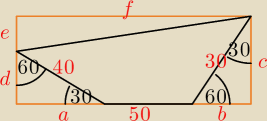
Red: Z trójkąta 30^o, 60^o, 90^o: d = 20, a = d√3 = 20√3, b = 15, c = b√3 = 15√3, e = c − d = 15√3 − 20, f = 20√3 + 65

	1
Pole czworokąta P = c*f −		*(a*d + b*c + e*f)
	2

daras: eleganckie rozwiązanie Red

Blue: Czy przekątna w tym drugim przykładzie powinna wynosić 10√45+12√3

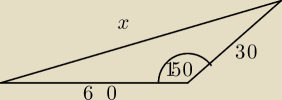
Kacper: Na początek policzymy wartość cos150

	√3
cos150=cos(180−30)=−cos30=−
	2

Teraz tw. cosinusów

	√3
x2=602+302+2*30*60*
	2

x²=3600+900+1800√3 x²=4500+1800√3 x=√4500+1800√3=√900(5+2√3)=30√5+2√3 O to chodziło?

Blue: a, rzeczywiście tam źle pomnożyłam 30 *60 haha xD dzięki. I teraz kąt pomiędzy 50 a 40 z cosinusów i pola dwóch trójkątów tak?

Blue: czy ten drugi kąt będzie miał ok 152 stopnie?

Blue: Wyszło dobrze! Wreszcie, dzięki wielkie Wszystkim za pomoc !