granica bezendu: Oblicz granice

	sin n
limn→∞		?
	n

asdf: 0

MQ: 0≤sin n≤1

MQ: Miało być oczywiście −1<=sin<=1

asdf:

	1
sin(n) oscyluje miedzy (−1;1), a		→ 0
	n

asdf: Jeśli ciągi (a_n) i (b_n) są zbieżne oraz a_n ≤ b_n dla każdego naturalnego n, to \lim a_n ≤ lim~b_n. Jeśli ciągi (a_n),\; (b_n) są ciągami zbieżnymi odpowiednio do a oraz do b, to wykonalne są działania: \lim~(a_n + b_n) = a + b, \lim~(a_n − b_n) = a − b, \lim~(a_n * b_n) = a * b, \lim~a_n/b_n = a/b, o ile tylko b \ne 0 oraz b_n \ne 0 dla każdego n. no i sie przyjrzyj temu: http://pl.wikipedia.org/wiki/Granica_ci%C4%85gu#Przyk.C5.82ady

asdf: slashe ignoruj, z wiki skopiowane po prostu: http://pl.wikipedia.org/wiki/Granica_ci%C4%85gu#W.C5.82asno.C5.9Bci

bezendu: A można krok po kroku bo wynik to mi wolfram pokaże. ?

jakubs: A jakby to zrobił tak: −1≤sin n≤1

−1		sin n		1
	≤		≤
n		n		n

	sin n
Czyli limn→∞		=0
	n

asdf: przeciez masz krok po kroku...

Mila: http://www.matemaks.pl/granica-ciagu.php?tid=10101

bezendu: Dziękuję, będę analizował bo utkwiłem na razie w punkcie

Mila: sin(n )− ciąg ograniczony

	1
limn→∞(		)=0 ⇔
	n

	1
limn→∞(sin(n))*(		)=0
	n

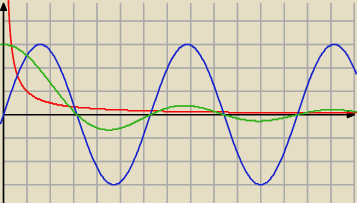
Trivial: bezendu, zerknij na obrazek, a zaraz zobaczysz dlaczego tak jest. 1/x, 3sinx, (3sinx)*(1/x)

asdf: na jakim punkcie utwiłes?

bezendu: na granicach ciągów związanych z trygonometrią.

Trivial: To nie jest bezpośrednio związane z trygonometrią. Przykład analogiczny bez trygonometrii:

	(−1)n
Znajdź granicę ciągu an =		.
	n

bezendu: To nie bardzo wiem jak

	1
jak by było an=(1+		)n to by było pięknie
	n

Trivial: bezendu, włącz intuicję proszę.

bezendu: To tutaj też lim=0

Trivial: Tak. Dlaczego?

asdf: czemu?

bezendu: Ponieważ ciąg jest rozbieżny ?

Trivial: Nie.

bezendu: Zbieżny a nie rozbieżny.

Trivial: Nie.

bezendu: jak by obliczając kolejne wyrazy tego ciągu to dla parzystych wychodzą dodatnie wyrazy dla nieparzystych ujemne ale w obu przypadkach wyrazy ''idą'' do 0 ? Ja tak to rozumiem.

Trivial: bezendu, oczekiwałem sposobu z ciągiem ograniczonym i zbieżnym do zera, ale Twój sposób też jest OK.

WueR:

(−1)n		1
	= (−1)n*
n		n

1
	jest zbiezny i wraz ze wzrostem argumentow wartosci sa coraz mniejsze. Te wartosci
n

mnozymy pozniej przez −1 oraz 1 na zmiane...wiec w efekcie dostajemy za kazdym kolejnym razem cos mniejszego od 1 lub wiekszego od −1 coraz bardziej zblizajac sie do zera. Ogolnie jest takie twierdzenie, ze jesli x_n jest ograniczony i y_n→0, to x_n*y_n rowniez dazy do zera.

bezendu: A mogę wiedzieć jak to twierdzenie się nazywa ?

Trivial: http://www.matemaks.pl/granica-ciagu.php?tid=10101

bezendu: Dzięki

Mila: No, dopiero Trivialowi uwierzył?

asdf: jak chcesz kolejne, bo widziałem juz ogarniales liczbe e:

	√n3
limn→∞
	1   33√n27*(1− )ctg(n)   tg(n)

bezendu: Nie kliknąłem w Twój link Mila ale mam do Ciebie pełne zaufanie !

bezendu:

√n3
−1   33√n27*[(1+ )tg(n)]ctg(n)/tg(n)   tg(n)

	√n3
limn→∞
	33√n27*(e−1)ctg(n)/tg(n)

	ctg(n)
i teraz muszę policzyć limes z tego		?
	tg(n)

Trivial: asdf, z ogromną przyjemnością zobaczę jak rozwiązujesz ten przykład.

bezendu: Trivial dobrze myślę ?

Trivial: Dlaczego zastosowałeś przejście z "e"? 1/tg(n) nie dąży wcale do zera. Osobiście nie wiem jak rozwiązać ten przykład.

Trivial: Zresztą ten problem jest źle postawiony, gdyż można wybrać np. takie n (dowolnie duże), że tg(n) ≈ 0.1 i wtedy zapisane wyrażenie nie ma sensu matematycznego.

WueR: Nalezy pamietac, ze "wzor na granice z e" mozna stosowac tylko wtedy, gdy we wzorze

	1
(1+		)n, xn→∞ (gdzie xn to ciag).
	xn

bezendu: To jak to rozwiązać Panowie ?

Trivial: Jeżeli jeszcze tego nie wywnioskowałeś: nie da się.

bezendu: A ja jakieś kombinacje z liczbą e

Mila: Rozwiązuj zadania z poręcznika , zbioru. W Krysickim są dobre zadania dla początkujących.

bezendu: Zamówiłem sobie tą książkę bo wolę wersję drukowaną niż pdf

Mila: tg(n) nie ma granicy w nieskoczoności.

WueR: Ale wiecej ksiazek nie zamawiaj. W bibliotece bedziesz mial tyle pozycji matematycznych, ze w zyciu nie zdazysz przerobic, a tam za darmo mozna wypozyczac.

bezendu: Ok, ale teraz w domku sobie popracuję z tą książką

5-latek: Szkoda ze nie mowiles ze potrzebujesz bo mam w domu 2 pierwsze czesci Krysickiego

asdf: hehe

bezendu: Spokojnie, stać mnie na książki. A lepiej zostaw sobie bo mogą Ci się przydać

5-latek: To ze stac cie na ksiazki to wiem bo pracujesz . Tak naprawde to mi sie juz nie przydadza (zostawie sobie jedna ) na pamiatke bo ja sie z nich uczylem

Piotr 10: Chętnie bym wział lub kupił 5−latek tą książkę Krysickiego Ta książka to analiza matematyczna Ja będę później jak coś, bo jadę do Warszawy papiery złożyć