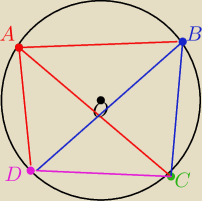
okrag kolo 4 5-latek: W okregu o promieniu r wybrano 4 punkty A B C D (rozne ) Kazde dwa z tych punktow sa koncami sa a koncami pewnej cieciwy a) Ile jest takich cieciw ? b) Jakiej lliczby nie przekracza suma dlugosci tych cieciiw niezaleznie od polozenia punktow A B C D w okregu ? c) Rozwiaz zadanie gdy jest danych n roznych punktow w okregu Wiec tak a) bedzie 6 takich cieciw w b) nie wiem jak to mam rozpatrywac bo mam sie powolac na tweirdzenie ktore mowi ze odleglosc 2 punktow (dowolnych) kola o promiemiu r nie jest wieksza od 2r. Wobec tego ta dlugosc (ale jednej cieciwy) nie przekracza 2r . TYlko ze tutaj jest napisane ze suma dlugosci tych cieciw (wiec ja zrozumialem ze tych 6 cieciw ) a ta bedzie wieksza niz 2r .

	n−1
Co do c ) to tych cieciw w okregu bedzie		*n i tez dlugosc jednej cieciwy nie
	2

przekroczy 2r

Janek191: b ) L < 6*2r = 12 r

Janek191: c) L < 0,5*(n −1)*n*2 r = ( n −1)*n*r

5-latek: WItam Janek Pisalem nastepne zadanie wiec dopiero teraz odpisuje czyli tak nalezalo podejsc do tego zadania? Ja to rozumie teraz . Dziekuje za wyjasnienie