logarytmy
tyu:
| | 2 | | 5 | |
( |
| )log0,25(x2−5x+8) ≤ |
| |
| | 5 | | 2 | |
| | 2 | | 2 | |
( |
| )log0,25(x2−5x+8) ≤ ( |
| )−1 |
| | 5 | | 5 | |
teraz nie zmieniam znaku nierówności i porównuje wykładniki
log
0,25(x
2−5x+8)} ≤ −1
log
0,25(x
2−5x+8)} ≤ log
0,254
tu opuszczam znak logarytmu i mieniam znak nierówności na przeciwny, bo to f. malejąca
x
2−5x+8 ≥ 4 x
2−5x+4 ≥ 0 x=1 x=4
x∊(−
∞;1>u<4;+
∞)
dziedzina x
2−5x+8> ale tu nie ma miejsc zerowych, więc x∊R
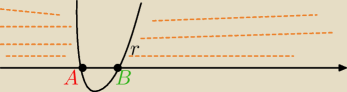
rys. A=1 B=4 (mała literka "r" stoi tam przez pomyłkę)
gdzie popełniłem błąd, bo prawidłowa odpowiedź to x∊<1;4>


