lamana
5-latek:
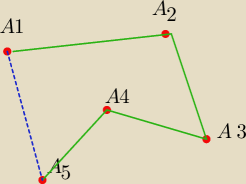
Udowodnij ze dlugogosc lamamnej A
1 A
2 A
3 A
4 A
5 jest wieksza od dlugosci odcinka A
1 A
5 .
Czy podobna wlasnosc przysluguje kazdej lamamej zwyczajnej . Wypowiedz ogolne twierdzenie
11 lip 18:02
MQ: Wystarczy udowodnić, że A1A2a5 jest dłuższe od A1A5.
11 lip 18:10
5-latek: A
1A
3<A
1A
2+A
2A
3
A
3A
5<A
3A
4+A
4A
5
A
5A
2<A
5A
1+A
1A
2 tylko co mi to da
11 lip 18:16
Mila:
Łamaną zwyczajną nazywamy taką łamaną, której dwa kolejne odcinki nie leżą na jednej prostej i
żadne niekolejne odcinki nie przecinają się.
W łamanej zwyczajnej zamkniętej A1=A5, ⇔|ł|>0
W łamanej zwyczajnej otwartej A1A5 jest bokiem wielokąta, jego długość jest mniejsza od sumy
długości pozostałych boków.
11 lip 18:18
MQ: No to inaczej:
A1A2A3>A1A3
A3A4A5>A3A5
A1A3A5>A1A5
widać, że
A1A2A3A4A5>A1A5
11 lip 18:20
MQ: @Mila w tym problemie nie musimy mieć aż takiego silnego założenia (łamana zwyczajna).
Wystarczą tylko dowolne trzy punkty niewspółliniowe.
11 lip 18:23
5-latek: Dzieki
MQ
czyli jesli mamy 3 punkty niewspoliniowe A
5 A
1, A
2 na plaszczyznie to korzystamy z takiej
wlasnosci ze A
1A
5<A
1A
2+A
2A
5
11 lip 18:25
MQ: No, z definicji trójkąta.
11 lip 18:29
5-latek: dziekuje rowniez Tobie
Milu 
Za dlugo pisalem a tu Wasze wpisy
MQ przepraszam Cie ale pominalem w zadaniu przez nieuwage w pisaniu ze jest napisane
(dlugosc lamamnej zwyczajnej.
czyli korzystamy z tzw nierownoswci trojkata i po problemie
11 lip 18:32
5-latek: A jeszce jedno jesli mozna
jesli bedziemy mieli lamamna zamknieta to wtedy juz wiadoma ze A1A5 jest mniejszy od
dlugosci tej lamanej bo wtedy odcinek A−1A5 to odcinek zerowy
11 lip 18:34
MQ: To ja nie zauważyłem, że w treści było jednak wspomniane o łamanej zwyczajnej.
Ale, jak powtarzam, nie trzeba aż tak silnego założenia.
11 lip 18:42
5-latek: Wiec tak: podobna wlasnosc przysluguje kazdej lamamnej zwyczajnej
Ogolne twierdzenie mozna wypowuedziec w nastepujacy sposob : dlugosc boku lamanej zwyczajnej
(niew wiem jak go tutaj nazwac) jest mniejsza od dlugosci wszystkich jej bokow
11 lip 18:42
MQ: Można silniej:
Długość każdego boku łamanej zwyczajnej zamkniętej jest mniejsza od sumy długości pozostałych
jej boków.
Lub tak:
Odległość początku od końca łamanej zwyczajnej otwartej jest mniejsza od jej długości.
11 lip 18:47
5-latek: Dziekuje jeszce raz i zycze milego popoludnia
11 lip 18:49