Funkcja Liniowa Ewelina ;): Napisz wzór funkcji liniowej f, której wykres przechodzi przez punkt P= (−2,3) i jest równoległy do wykresu funkcji g. a) g(x)= −5x+1 b) g(x)= 2−1,5x c) g(x)= −1,5 bardzo proszę o pomoc , odwdzięczę się!

zainteresowany: a jak się odwdzięczysz?

Kaja: a)funkcje liniowe, których wykresy sa prostymi równoległymi maja taki sam współczynnik kierunkowy (czyli to a stojące przed x), czyli wzór funkcji f, to y=−5x+b. teraz aby wyliczyc to b, wystarczy podstawić do tego wzorku współrzędne punktu P: 3=−5*(−2)+b 3=10+b b=−7 a więc wzór funkcji to: y=−5x−7

zainteresowany: y = a(x − x₀) + y₀ y = −5(x + 2) + 3 y = −5x − 7

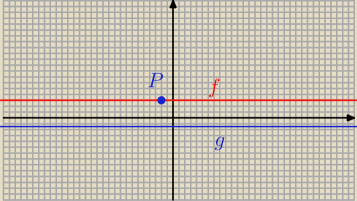
Janek191: c) g(x) = − 1,5 P = ( − 2; 3) więc f(x) = 3 =======

Dziadek Mróz: Dla f(x) = ax + b_f funkcja g jest równoległa gdy g(x) = ax + b_g Dla f(x) = ax + b_f funkcja g jest równoległa i przechodzi przez punkt P(x_p, y_p) gdy g(x_p) = y_p ax_p + b_g = y_p b_g = y_p − ax_p g(x) = ax + b_g

bum: "funkcja równoległa" ? ... co to za bełkot?

asystent: Cały wywód Dziadka Mroza jest bełkotliwy, może odstraszyć i zniechęcić do nauki matematyki nie tylko Ewelinę, a Janek 191 wciąż nie nauczył się stosować większe kratki przy rysowaniu układu współrzędnych. Znacie przysłowie: "uczył Marcin Marcina ... "?

Hajtowy: Uczył Marcin Marcina, a sam głupi jak świnia ?