| ds | ||
∫∫ | , gdzie S: x2+y2=81; 0 ≤ z ≤ 9 | |
| x2+y2+z2 |
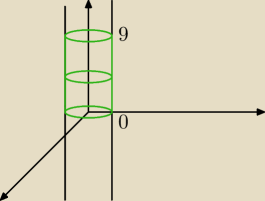 No jest coś takiego.
Tylko właśnie czy ta całkę mam liczyć dla powierzchni bocznej walca czy też podstaw?
Dla podstaw to w sumie nie jest specjalnie trudne bo za funkcje
z=f(x,y), wstawiam 0 lub 9
Ale jak mam wyznaczyć funkcje z tej powierzchniowi bocznej?
Czy to jednak inaczej trzeba (tylko bez całki potrójnej)?
No jest coś takiego.
Tylko właśnie czy ta całkę mam liczyć dla powierzchni bocznej walca czy też podstaw?
Dla podstaw to w sumie nie jest specjalnie trudne bo za funkcje
z=f(x,y), wstawiam 0 lub 9
Ale jak mam wyznaczyć funkcje z tej powierzchniowi bocznej?
Czy to jednak inaczej trzeba (tylko bez całki potrójnej)?
 w mojej skromnej opinii trzeba zastosować twierdzenie Greena−Gaussa−Ostrogardzkiego, żeby
zamienić całkę powierzchniową na potrójną.
Jednak zastosowanie twierdzenia 'na sucho" troche zmasakruje funkcje podcałkową, dlatego
najpierw przeszedłbym w układ współrzędnych walcowy, i pozamieniał wszystkie x2+y2 na r2.
Następnie zastosował GGO.
A potem wrzucić granice całkowania i przecałkować nową funkcję podcałkową, nie powinno tam być
żadnych ograniczeń funkcjami innymi.
Tyle że miałem to bardzo słabo obrabiane niestety, większość semestru analizy II nie dała tyle
co bym chciał, dlatego jak tak nie można to niech ktoś da znać żebym nie pisał bzdur
w mojej skromnej opinii trzeba zastosować twierdzenie Greena−Gaussa−Ostrogardzkiego, żeby
zamienić całkę powierzchniową na potrójną.
Jednak zastosowanie twierdzenia 'na sucho" troche zmasakruje funkcje podcałkową, dlatego
najpierw przeszedłbym w układ współrzędnych walcowy, i pozamieniał wszystkie x2+y2 na r2.
Następnie zastosował GGO.
A potem wrzucić granice całkowania i przecałkować nową funkcję podcałkową, nie powinno tam być
żadnych ograniczeń funkcjami innymi.
Tyle że miałem to bardzo słabo obrabiane niestety, większość semestru analizy II nie dała tyle
co bym chciał, dlatego jak tak nie można to niech ktoś da znać żebym nie pisał bzdur
