czy ktoś jeszcze mi pomoże michał: rozwiąż równanie cos(^2π_x) + ¹₂x² = 2x − 3

Janek191:

	2 π
Tam jest cos (		) ?
	x

Janek191:

	2π		1
cos (		) = −		x2 + 2x − 3
	x		2

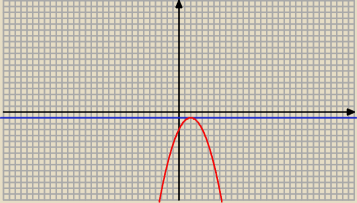
a = − 0,5 < 0 − ramiona paraboli skierowane są ku dołowi

	− 2
p =		= 2
	2*(−0,5)

q = − 0,5*2² + 2*2 − 3 = − 2 + 4 − 3 = − 1 W = ( 2 ; − 1)

	2π
oraz − 1 ≤ cos(		) ≤ 1
	x

	2π
dla x = 2 cos(		) = cos π = − 1
	2

Odp. x = 2 ========

michał: dziękuję bardzo

pigor: ..., rozwiąż równanie cos(^2π_x)+¹₂x²=2x−3. a ja widzę to w swojej szufladzie takie rozwiązanie : cos(^2π_x)+¹₂x²=2x−3 ⇔ cos(^2π_x) = −¹₂x²+2x−3, a takie równanie może mieć rozwiązanie (o ile istnieje) ⇔ ⇔ |−¹₂x²+2x−3|≤ 1 ⇔ |−¹₂(x²−4x+6)|≤ 1 ⇔ ¹₂|x²−4x+4+2|≤ 1 ⇔ ⇔ |(x−2)²+2|≤ 2 ⇔ (x−2)²+2≤ 2 ⇔ (x−2)²≤ 0 ⇔ x−2=0 ⇔ ⇔ x=2 − dziedzina d. równania, więc i ... jego rozwiązanie.