Jak obliczyć takie równanie? Maciej: |2x + 3| = x + 1 Jak obliczyć takie równanie?

ula: Równań się nie oblicza , równania się rozwiązuje

Piotr 10: Założenie: x+1 ≥ 0 L_s ⋀ P_s ≥ 0, a więc I2x+3I² = (x+1)² i liczymy 'ukochaną deltę''

Maciej: Dzięki. Ja chcę tylko się tego nauczyć….

Piotr 10: Lub drugi sposób: Założenie: x+1 ≥ 0 ,a więc 2x+3=x+1 v 2x+3 = −(x+1)

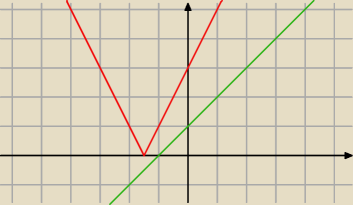
s: Możesz sobie też to narysować i wywnioskować, że nie masz tutaj rozwiązań.

Maciej: A to nie powinno być tak? 2x+3=x+1 v −(2x+3) = x+1

Piotr 10: Ale to jest to samo

Piotr 10: −(2x+3)=x+1 * (−1) 2x+3 = − (x+1)

Maciej: bosze…. ostani raz miałem mate 1998… czyli x=−2 oraz x= −4/3 Powinienem to jeszcze odnieść jakość do tego co mi wychodzi z 2x+3=0?

Piotr 10: A po co teraz sie uczysz ? Dobra wyszły Ci dwa rozwiązania: x= − 2 x = − 4/3 I2x+3I=x+1 wstaw za iksa te cyfry i wyjdzie Ci sprzeczność Najlepiej napisać założenie odrazu: x+1 ≥ 0 x ≥ − 1

ula: @[Macieja]] Czyli "umiałeś już chodzić i biegać" .... i znowu "raczkujesz"?

Maciej: Raczkuje − zdecydowanie. Ale jest coraz lepiej. Przed czterdziestką wsztstko zakumam.

ICSP: dla dowolnego rzeczywistego x |2x + 3| = | x + 2 + x + 1| ≥ |x + 2| + |x + 1| ≥ |x| + |x + 1| + |2| > |x + 1| ≥ x+ 1 stąd : |2x + 3| > x + 1 równanie jest równaniem sprzecznym.

unknown: pokazał to s o godz.: 23:01