Wzajemne położenie prostej i okręgu Madzz: Wzajemne położenie prostej i okręgu Napisz równania stycznych do okręgu o i przechodzących przez punkt A jeśli o: x²+y²+6x+2y+5=0 A(−2,2) Hmm czy może mi ktoś pomóc rozwiązać to zadanie? Musze zrobić drugim sposobem a zrobiłam tylko jednym...mianowicie skorzystałam z wzoru na odległośc srodków okręgu...wyszło mi prawidłowo...ale potrzebuje rozwiazanie tego zadania poprzez układ równań. Nie bardzo wiem jaki do końca mam ułożyć.Bo jak układam to mi źle wychodzi. Proszę o pomoc !

Madzz:

SC: pomogę

Madzz: Dziękuję Pierwsza prosta to y=¹₂+3 a druga to y=−2x−2

SC: prosta przechodząca przez punkt A 2=−2a+b zatem mamy b= 2+ 2a otrzymujesz układ równań z parametrem: y=ax+2+2a i równanie okręgu wstawiając do równania okręgu za y otrzymujemy równanie kwadratowe z 1 niewiadoma x i parametrem a teraz należy odpowiedzieć kiedy to równanie ma dokładnie jedno rozwiazanie za moment wrzucę częściowo rozpisane

SC: x²+(ax+2+2a)²+6x+2(ax+2+2a)+5=0

SC: x²+(ax+2+2a)²+6x+2(ax+2+2a)+5=0

SC: mam kłopot z transferem

SC: x² + a² x² + 4 + 4 a² + 4ax +8a + 4a² x + 6x + 2ax +4 +4a + 5 = 0 proszę kontrolować, czy umiem mnożyć i dodawać

Madzz: No właśnie dokłądnie takie ułożyłam i mam kłopot ze zrobieniem tego wiem ze to zadanie jeste prymitywne ale kurcza nie wychodzi mi to potegowanie cos źle robie

Madzz: no włąsnie i tak miałam cos takiego i ja nie umiem sobie tego skrócić

SC: i mamy (1+a²) x² +(4a² + 6a +6) x + 4a² + 12a + 13 = 0

SC: i mamy (1+a²) x² +(4a² + 6a +6) x + 4a² + 12a + 13 = 0

SC: zatem mamy równanie kwadratowe, które ma mieć dokładnie jedno rozwiązanie ponieważ 1 + a² > 0 dla a∊R, zatem Δ = 0

Madzz: dobra jestem zbyt głupia zeby to rozwiazac co z tego mozna wyznaczyc?

Madzz: aaaaaaaaa teraz juz rozumiem !

Madzz: heh dziękuję bardzo dziękuje za pomoc

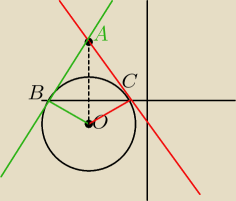
ak1: Nie wiem czy wyszedł rysunek Styczne do okręgu i przechodzące przez punkt A to po prostu okrąg wpisany w kąt. Z równania okręgu wyznaczamy wsp. jego środka i promień. Obliczamy długośc odcinka |AO|, odcinek |CO| to promień okręgu. Z Pitagorasa liczymy długośc odcinka |AC| a następnie wsp. punkyu C. Teraz już tylko ułożu równwnie prostej przechodzącej przez dwa punkty A iC. Druga prosta przechodzi przez punkty A i D długośc odcinka |AB|=|AC| i liczymy tak samo.

Madzz: O też siwtny pomysł na roziwazanie tylko nauczycielka wmaga tego powyzej dziekuje Wam

SC: proszę to koniecznie po mnie przeliczyć/sprawdzić Δ=(4a² + 6a +6)² − 4 (1+a²)(4a² + 12a + 13) = =16a⁴ + 36 a² + 36 + 48a² + 48a³ + 72a − 16a⁴ − 48a³ − 52a² − 16a² −48a − 52

SC: dokończyć, czy poradzisz sobie Madzz?

Madzz: Wiem..ze może Cię wykorzystuje i marnuje Twój cenny czas ale jak byś mógł?mogła dokonczyc? bo potem źle zrobie i bedzie a tak to bede miała pewnosc i dzieki Tobie nie dostane jedynki

SC: tylko jak pisałam − sprawdź − bo dla mnie 2 + 2 może być na przykład 5 Δ=16a² + 24 a − 16

Madzz: dobrze sprawdze i bardzo dziekuje jeszcze raz

SC: 16a²+24a−16=0 / :8 2a² +3a − 2=0 Δ₁ = 9+16 = 25

	1
a1 = (−3−5)/4 = −2 a2 = (−3+5)/4 =
	2

zatem wyznaczam dla a₁ b = 2 + 2*(−2)=−2

	1
dla a2 b = 2+ 2*		= 3
	2

i możesz podstawić do wzoru na prostą

	1
y = −2x −2 oraz y =		x + 3
	2

Jak widać są to Twoje odpowiedzi

Madzz: Dzięki wielkie też chce być taka mądra jak wy tu wszyscy na tym forum hehe