Uzupełniam braki. bezendu: Jak to obliczyć NWD( 24! i 24⁸ ) ?

MQ: Rozbij sobie 24! i 24⁸ iloczyny potęg liczb pierwszych.

bezendu: Już chyba wiem, dziękuję.

Maslanek: 2²²*3⁸

Mila: 1) 24⁸=(3*2³)⁸=3⁸*2²⁴ 2)Ile będzie 2 w iloczynie 24! ? [..] część całkowita

	24
[		]=12
	2

	24
[		]=6
	4

	24
[		]=3
	8

	24
[		]=1
	16

12+6+3+1=22 Ile będzie 3 w iloczynie 24! ?

	24
[		]=8
	3

	24
[		]=2
	9

8+2=10 NWD(24!, 24⁸)=2²²*3⁸

bezendu: Czemu liczysz to za pomocą [ ] ? Już mnie przeraża myśl studiowania.

ula:

Mila: To tak się liczy. Jak Ty liczyłeś? Oblicz ile zer ma na końcu 100!

bezendu: Szczerze to tylko rozłożyłem tak jak Maślanek i myślałem dalej.

Maslanek: Ja też widzę pierwszy raz ten sposób Ale powiem, że bardzo ciekawy Mogłabyś przybliżyć albo podrzucić jakiś link, Mila? Bo nie mam pojęcia nawet w czym tego szukać

Mila: Nie przerażaj się, do wszystkiego można się przyzwyczaić, pokonać trudności. To była mała liczba, trzeba znaleźć zasadę. Pomyśl z 100!

sushi_ gg6397228: tylko nie każ mu rozpisywać "10!" w postaci ustawiania osób, bo mu życia nie starczy

bezendu: 100!

	100
[		]
	5

	100
[		]
	2

chyba coś nie tak...

Maslanek: Raczej byśmy liczyli ilość dwójek: Kolejno: [100/2] ; [100/4]; [100/8]; [100/16]; [100/32]; [100/64] Potem liczbę piątek: Kolejno: [100/5]; [100/25] Dziesiątki występują już w rozkładzie na dwójki i piątki, więc nie ma sensu ale nie wiem czemu tak

Mila: Dwójek jest na pewno więcej niż piątek, liczysz ile będzie piątek, bo 2*5=10 masz jedno zero z każdej takiej pary. Czekam.

bezendu: Ja nie wiem nic z tego teraz kompletnie zielony ! A to dopiero druga część kursu..

Maslanek: Zgadzałoby się Liczę Maplem sumy dla treningu (może ogarnę kiedyś komendy i nie będę szukał po netach) Ale czemu akurat tak?

bezendu: Chętnie bym więcej czasu zagospodarował ale go nie mam. Czemu liczę tylko ilość ''5'' ?

Maslanek: http://pl.wikipedia.org/wiki/Silnia Tu jest tylko twierdzenie, poszukam dowodu

Maslanek: Nie tylko. Liczysz ilość dwójek i piątek. Ich iloczyn daje 10, zatem jedno 0 na końcu liczby wyjściowej. Czyli min (ilość "2", ilość"5") daje Ci liczbę zer na końcu liczby będącej wynikiem silni

Mila: Czytaj mój wpis 22:34.

bezendu:

	100
[		]=20
	5

I co dalej ?

Mila:

	100
[		]=4
	52

i koniec, bo 100 nie dzieli się przez 5³=125. 100! ma na końcu 20+4=24 zera. http://www.wolframalpha.com/input/?i=factor+100%21

Maslanek: Nie mogę znaleźc dowodu

bezendu: Nie rozumiem czemu 5² a nie 5 ?

MQ: Bo 5 już policzyłeś ty. Zauważ, że Mila uwzględnia zarówno twoje 100/5 jak i 100/5² Po prostu pytałeś "co dalej?", więc zrobiła tylko "dalej".

bezendu: Dziękuję. Muszę już uciekać, jutro do tego wrócę. Dobranoc.

Mila: W iloczynie 100! wystapią następujące liczby podzielne przez 5: 5,10,15,20,25,30,35, 40,45,50,55,60,65,70,75,80,85,90,95,100 masz 20 liczb 1) dzielimy przez 5 100:5=20 i to nie jest wszystko 2) Zauważ, że w rozkładzie na czynniki pierwsze liczb : 25,50,75,100 występują dwie piątki ( jedną już uwzględniliśmy), teraz liczymy ile jest tych drugich Zatem dzielimy 100:5²=100:25=4 Łącznie mamy 20+4=24 piątki w rozkładzie liczby 100! na czynniki pierwsze. Co druga liczba jest parzysta, wię mamy więcej dwójwk niż piątek, Każda para 2 i 5 daje jedno zero w iloczynie 2*5, stąd 100! ma 24 zrea na końcu.

fx: Mila! Ja Cię kocham . Już po raz drugi ułatwiłaś mi życie. Nigdy nie wpadłem na Twój sposób.

Trivial: Wydaje mi się, że już kiedyś mówiłem o tym sposobie, ale nie mogę znaleźć tamtego tematu.

zawodus: Można takie zadania znaleźć w książkach pana Pawłowskiego dla olimpijczyków

zombi: Taaak, sam z Pawłowskiego to robiłem + na jakimś konkursie miałem. Było coś takiego: Iloma zerami kończy się liczba 2012! albo 2013! bo nie pamiętam, który to rok.

zawodus: Co roku zmieniają tylko liczbę Niemniej jednak ciekawe zadanie

bezendu: Mi daleko do olimpijczyka...

bezendu: jakiś inny przykład ?

ula: 1 000 000 !

bezendu: O kurde..

Mila: 24 99 98 zer.

ula:

ula: 200 000 40 000 8 000 1 600 320 64 12 2 +−−−−−−− .............

bezendu: To chyba jest dla pasjonatów albo szaleńców.

ula:

Mila: No przecież znasz zasadę. To stosuj . Dzielisz kolejno przez 5, 5²,5³, .. az dojdziesz do sytuacji, że 1000 000 nie jest podzielne przez pewną liczbę 5^k. Eta wypisała kolejne wyniki.

bezendu: No właśnie nie mogę zrozumieć tej zasady.. I dlatego prosiłem o inny przykład.

Mila: Przeczytaj dwa razy ze zrozumieniem komentarz 23:26. Matematykę kończą studenci, którzy rozumieją co się do nich mówi, a jeśli w pierwszej chwili nie rozumieją to starają się zrozumieć po przyjściu do akademika czytając kilka razy wykład vel rozwiązane zadanie na ćwiczeniach, omawiają problem z kolegami, koleżankami. Tu masz ćwiczenia. 1) 20! 2) 30!

asdf: @Milu nie tylko matematykę, każdą rzecz, do której podchodzą z zamiłowaniem

Mila: Dziękuję asdf, ale, myślę, że bezendu obraził się.

asdf: nie ma o co − szczera prawda

daras: @zawodus z Toronto jesteś czy Pawłowski wpadł ci przypadkiem w ręce ?

bezendu: Nie obraziłem się

zawodus: A jaki ma związek Toronto z Panem Pawłowskim?

zorba: W "Toronto" są 2 t , w "Pawłowski" są 2 w

zawodus: To dla mnie zbyt skomplikowane

Mila:

Mila: bezendu, nie liczy ile jest zer?

bezendu: Jak bym wiedział to bym to policzył ?

	20
[		]=10
	2

	20
[		]=4
	5

14 ?

Mila: 1) Narysuj wykres funkcji: f(x)=[sin(x)] 2) rozwiąż równanie :

	3x−4
[x+3]=
	2

bezendu: http://pl.wikipedia.org/wiki/Pod%C5%82oga_i_sufit zgodnie z tym to będą punkty {−1.0,1} ?

Mila: Dlaczego liczysz dwójki? W iloczynie 20! co drugi czynnik jest parzysty ( podzielny przez 2), natomiast piątek jest dużo mniej i trzeba policzyć ile jest piątek w rozkładzie na czynniki pierwsze. Każdy iloczyn 2*5=10 daje jedno zero 20:5=4

	20
[		]= 0
	25

masz 4 piątki, to będą 4 zera na końcu . Możesz policzyć ile będzie dwójek w rozkładzie na czynniki pierwsze liczby 20!. 20:2=10 20:4=5 [20:8]=2 [20:16]=1 [20;32]=0 10+5+2+1=18 A ile trójek? [20:3]=6 [20:9]=2 [20:27]=0 6+2=8 20!=2¹⁸*3⁸*5⁴*.... itd można szukać aż do czynnika 19.

Mila: Rozpisz [sinx] w przedziale <0,2π>

bezendu: sin(x) 0 dla [0,π] −1 dla (π,2π) ?

Mila: No to nie jest całkiem dobrze. [sinx]= −1 dla sinx∊<−1,0) = 0 dla sinx∊<0,1) = 1 dla sinx=1 Teraz zapisz bez pominięcia jednego elementu. [sinx]=−1 dla x∊(π,2π) =0 dla ....... = 1 dla

bezendu: albo 0 albo −1 będzie ta funkcja przyjmować takie wartości ?

Mila:

	π
A dla		?
	2

bezendu: π/2 jest 1

Mila: To proszę o wykres.

Mila: f(x)=[sinx] dla x∊<0,2π> Czyli ma być: [sinx]=−1 dla x∊(π,2π)

	π		π
=0 dla <0,		)∪ (		,π>∪{2π}
	2		2

	π
= 1 dla x=
	2

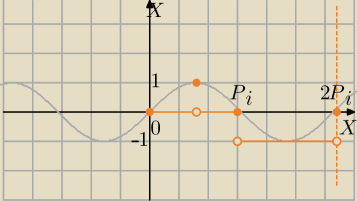
Mila: Pomarańczowy f(x)=[sinx] , x∊<0,2π>

bezendu: Już wiem gdzie miałem błąd.

Mila: Dobrze to wracamy do 30!, ile będzie zer na końcu?

Mila: Liczysz tylko, ile jest piątek w rozkładzie na czynniki pierwsze, reszta nie jest potrzebna. Pokazałam Ci wcześniej jak znaleźć rozkład na czynniki pierwsze dla liczby 20! Jeszcze raz tłumaczę. [30:5]=6 [30:5²]=[30:25]=1 [30:5³]=[30:125]=0 6+1=7 W rozkładzie na czynniki pierwsze liczby 30! jest 7 piątek, dwójek jest dużo więcej. 5⁷*2⁷=(5*2)⁷=10⁷ 30! ma 7 zer na końcu. To oblicz, ile zer ma na końcu 60!

bezendu: Jutro rozwiąże, dziś już idę spać. Dobranoc.

Mila: Miłych snów, człowieku pracy wakacyjnej. Poprosimy Marcina o rozwiązanie.

Saizou : 14 zer na końcu ma 60!

Mila: tak.

52: 80! ma na końcu 19 zer? Też się poduczę.

Trivial: 52, ile razy 80! dzieli się przez 10?

Mila: 52, zgadza się. No, to następne. Rozłóż na czynniki pierwsze 20!

Saizou :

bezendu: A możecie w innym temacie ?

Mila: Saizou, co to za minka?

Saizou : < tak > i już nie zaśmiecajmy posta bezendu

52: W rozkładzie na czynniki pierwsze liczby 20! jest 18 dwójek, 8 trójek, 4 piątki, 2 siódemki.

52: Sory bezendu

Mila: Czyli 20!=2¹⁸*3⁸* 5⁴*7²*.... i co dalej, ostatni czynnik to 19.

52: ...*11*13*17*19

Mila:

52:

bezendu: Może zajmę się innymi zadaniami a tę zostawię Wracam do granic

Mila:

5-latek:

PrzyszlyMakler: Odkopałem ten temat− nie ukrywam Milu, że szalenie mi pomógł i Twoja cierpliwość i dobre serce w tłumaczeniu nie znają granic <3. Sposób z zerami rozumiem [chyba] np 126! ile ma zer na końcu? 126:5³ =1,~~~ 126:5²= 5 126:5= 25 Czyli ta liczba ma 31 zer na końcu? I trochę mniej rozumiem rozkład na czynniki pierwsze, ale spróbuję np. 22! na czynniki pierwsze 22:2 = 11 22:4= 5,~~ 22:8= 2,~~ 22:16 = 1,~~ czyli 22! ma w rozkładzie 2¹⁹ 22:3= 7 22:9 = 2 to ma ona też 9 trójek= 3⁹ 22:5 = 4 czyli 5⁴ 22:7= 3 7³ 22:11=2 11² 22:17 = 1 22:19= 1 Czyyyylii 22! = 19*17*11²*7³*5⁴*3⁹*2¹⁹ Dobrze rozumuję?

Pytający: Dobrze rozumujesz, ale zapomniałeś o 13. I odkopałeś, i poczytałem, i również dziękuję Mili za jakże klarowne przedstawienie tegoż sposobu.

PrzyszlyMakler: a no tak.. szczęśliwa 13 #TeamMila

PrzyszlyMakler: A jak np. znaleźć liczbę dzielników liczby 3³*2⁴ ?

Pytający: Liczba dzielników 2⁴*3³ to (4+1)*(3+1)=20. Dzielniki 2⁴*3³=432: 2⁰*3⁰=1 2¹*3⁰=2 2²*3⁰=4 2³*3⁰=8 2⁴*3⁰=16 2⁰*3¹=3 2¹*3¹=6 2²*3¹=12 2³*3¹=24 2⁴*3¹=48 2⁰*3²=9 2¹*3²=18 2²*3²=36 2³*3²=72 2⁴*3²=144 2⁰*3³=27 2¹*3³=54 2²*3³=108 2³*3³=216 2⁴*3³=432

Adamm: http://www.math.edu.pl/liczba-dzielnikow

PrzyszlyMakler: Dziękuję! Przyda się

Mila: Znaleźć liczbę dzielników liczby: 432 432=3³*2⁴ Dzielnikiem liczby 432 będzie każda liczba postaci : 3^k*2^m gdzie k∊{0,1,2,3} i m∊{0,1,2,3,4} zatem mamy : 4*5=20 dzielników

Zonley: 52: W rozkładzie na czynniki pierwsze liczby 20! jest 18 dwójek, 8 trójek, 4 piątki, 2 siódemki. Szostek nie liczymy bo 2x3=6?

ite: Rozkład liczby złożonej na czynniki pierwsze oznacza zapisanie jej jako iloczynu liczb pierwszych.