Geometria
Blue: Dany jest trójkąt ABC, w którym A=(0,0) i B=(4,0). Wyznacz współrzędne wierzchołka C .
|AC|= 4
√2, kąt ACB = 30 stopni

Z tw. sinusów liczę sinα i wychodzi kąt przy wierzchołku B 45 stopni, tzn, że kąt przy
wierzchołku A wynosi 135 stopni.
Zatem współczynnik kierunkowy = −1 i co dalej

?
Podstawiam pod wzór na odległość punktów od siebie i nie wychodzi.... punkt C=(x,−x)?
Jak to wyliczyć

?

6 lip 16:29
Blue: a sorry tam będzie 105 stopni, a nie 135 xD a więc a = −tg75 = −√3−2 , C= (x, (−√3−2)x)
... mimo to nadal nie wychodzi..
6 lip 16:32
6 lip 16:39
jakubs: Nie wiem czy to by było dobre i proste rozwiązanie, ale wyznaczyć długość trzeciego boku i
obliczyć pole trójkąta, a później podstawić do wzorku, który jest w tablicach o ile dobrze
pamiętam.
6 lip 16:49
bezendu:
Masz podaną odpowiedź w zadaniu ? Podaj to zobaczę czy mi dobrze wyszło ?
6 lip 17:03
Blue: jakiego wzorku?
6 lip 17:04
Blue: Już podaję... chwileczkę...
6 lip 17:04
Blue: C= (2−2√3, 2+2√3) lub (2−2√3, −2−2√3) lub (2+2√3, 2−2√3) lub (2+2√3, −2+2√3)
6 lip 17:06
Blue: Bezendu jeśli masz dobrze, to bardzo Cię proszę o pomoc, wydawało mi się , że mam dobrą
koncepcję do tego zadania, a mimo to nic mi nie wychodzi..
6 lip 17:08
Blue: czekam....
6 lip 17:23
bezendu:
Mi wyszło inaczej zupełnie.
6 lip 17:48
6 lip 18:00
...:
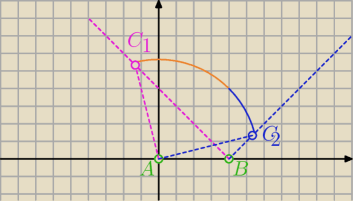
...itd
6 lip 18:03
Blue: Sorki, że odgrzebuję to zadanie, ale nadal nie mam rozwiązania, a wydaje mi się, że powinniśmy
tutaj skorzystać z tw. cosinusów , bo jest to w tym temacie, ale nie wiem, jak to
wykorzystać...
Może macie jeszcze jakieś pomysły?

9 lip 17:11
52: Z tw.cosinusów liczysz bok BC, C(x
C,y
C)
| | 1 | |
potem oblicz Pole trójkąta P= |
| sinα*a*b |
| | 2 | |
| | 1 | |
potem wynik pola przyrównujesz do wzorku P= |
| |(xB−xA)(yC−yA)−(yB−yA)(xC−xA)| |
| | 2 | |
Z tego ładnie powinno ci wyjść y
C, a potem wzór na długość odcinka BC i powinno wyjść x
c
9 lip 18:17
Mila:
Dany jest trójkąt ABC, w którym A=(0,0) i B=(4,0). Wyznacz współrzędne wierzchołka C ,
wiedząc,że
|AC|= 4√2, ∡ ACB = 30o.
1) rysunek jak u kolegi z 18:03, trzeba jeszcze uwzględnić odbicie symetryczne wzgledem osi OX
ozn. a=BC
2) z tw. cosinusów skorzystaj tak:
42=a2+(4√2)2−2*a**4√2*cos(30o)
otrzymasz a1,a2
3) rozwiązujesz uklady równań: (znajdujesz punkty przecięcia okręgów: ⇒C1, C1',C2, C2'))
(x−4)2+y2=a12
x2+y2=(4√2)2
(x−4)2+y2=a22
x2+y2=(4√2)2
i to już koniec problemu.
=================
Czekam na potwierdzenie rozwiązania.
9 lip 19:23
Blue: Mila , a powiedz mi dlaczego korzystamy z tych okręgów, bo właśnie mi z cosinusów wyszło, że
ten bok wynosi 2
√6−2
√2 lub 2
√6+2
√2, ale nie wiem co dalej... A tej Twojej metody za
bardzo nie rozumiem. Mogła byś mi ją wyjaśnić?

I przepraszam, że tak długo nie odpisywałam, ale było tak gorąco, że nie miałam siły żyć, a co
dopiero rozwiązywać zadanka

20 lip 11:16
Blue: Jak rozwiązuję te układy równan, to pierwsza współrzędna mi wychodzi dobrze, ale druga już
nie... nie wiem, dlaczego..
20 lip 11:27
pigor: ..., to może jeszcze tak :
niech
C=(x,y)=? , to z warunków zadania, tw. Pitagorasa i równania
z porównanie wzorów na pole Δ masz np. taki układ równań :
x2+y2=(4√2)2 i 12*4y= 12*4√2*√y2+(4−x)2*sin30o ⇔
⇔ x
2+y
2=32 i y=
12*
√2√y2+(4−x)2 ⇔ x
2+y
2=32 i 2y
2= y
2+(4−x)
2 ⇔
⇔ y
2=(4−x)
2 i x
2+(4−x)
2=32 ⇔ (*)
|y|=|4−x| i x
2−4x−8=0 ⇒
⇒ x
2−2x*2+4=12 ⇔ (x−2)
2= 4*3 ⇔
|x−2|=2√3 ⇔ x−2= ±2
√3 ⇔
⇔ (**)
x=2±2√3, stąd i z (*)
|y|=|4±2
√3|=
4±2√3 ⇒
⇒
C=(x,y)=2±2√3, 4±2√3 − szukane rozwiązanie (
4 punkty C)...

20 lip 14:27
Mila:
Trzeba to sobie wyobrazić geometrycznie− czynnościowo.
Punkty C leżą na okręgu o środku S=(0,0) i r=4√2
Obliczasz trzeci bok ΔABC z tw. cosinusów.
Wbijasz cyrkiel w punkt B i rysujesz okrąg o promieniu r=2√6−2√2 , otrzymasz dwa punkty
przecięcia z okręgiem x2+y2=(4√2)2
lub R= 2√6+2√2, też otrzymasz dwa punkty przecięcia z okręgiem x2+y2=(4√2)2.
Algebraicznie to oznacza rozwiązanie dwóch układów równań.
Nie wiem czy dobrze obliczyłaś długość trzeciego boku, bo dawno wyrzuciłam kartkę z rachunkami
do tego zadania.
20 lip 16:30
Blue: Pigor , Twoje rozwiązanie wydaje mi się bardziej zrozumiałe

Mogę po prostu zamiast tego
√y2+(4−x)2 podstawiać wartość tego trzeciego boku obliczonego z twierdzenia cosinusów

?
Tylko właśnie nie wiem, który wynik mam podstawić, bo mi wyszły obydwa dodatnie pierwiastki..
22 lip 00:42
 Z tw. sinusów liczę sinα i wychodzi kąt przy wierzchołku B 45 stopni, tzn, że kąt przy
wierzchołku A wynosi 135 stopni.
Zatem współczynnik kierunkowy = −1 i co dalej
Z tw. sinusów liczę sinα i wychodzi kąt przy wierzchołku B 45 stopni, tzn, że kąt przy
wierzchołku A wynosi 135 stopni.
Zatem współczynnik kierunkowy = −1 i co dalej ?
Podstawiam pod wzór na odległość punktów od siebie i nie wychodzi.... punkt C=(x,−x)?
Jak to wyliczyć
?
Podstawiam pod wzór na odległość punktów od siebie i nie wychodzi.... punkt C=(x,−x)?
Jak to wyliczyć ?
?

 ?
?
 ...itd
...itd

 I przepraszam, że tak długo nie odpisywałam, ale było tak gorąco, że nie miałam siły żyć, a co
dopiero rozwiązywać zadanka
I przepraszam, że tak długo nie odpisywałam, ale było tak gorąco, że nie miałam siły żyć, a co
dopiero rozwiązywać zadanka

 Mogę po prostu zamiast tego
√y2+(4−x)2 podstawiać wartość tego trzeciego boku obliczonego z twierdzenia cosinusów
Mogę po prostu zamiast tego
√y2+(4−x)2 podstawiać wartość tego trzeciego boku obliczonego z twierdzenia cosinusów ?
Tylko właśnie nie wiem, który wynik mam podstawić, bo mi wyszły obydwa dodatnie pierwiastki..
?
Tylko właśnie nie wiem, który wynik mam podstawić, bo mi wyszły obydwa dodatnie pierwiastki..