Oblicz objętość bryły gacek: Oblicz objętość bryły Bryła jest ograniczona: x²+y²+z²=4 oraz z=1, z=0 Ktoś ma pomysł jak się za to zabrać? (najlepiej jak najprościej się da)

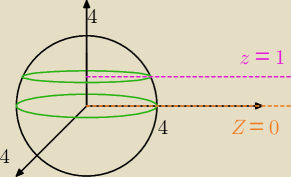
Ada: Na rysunku powinno być zaznaczone 2. z = rsinθ x = rcosφcosθ

	π		π
y = rsinφcosθ, dla r>0, θ∊(−		,		), φ∊(0, 2π)
	2		2

J = r²cosθ z równania: x²+y²+z² ≤ 4 ⇒ r² ≤ 4 ⇒ r∊(0,2) φ∊(0, 2π), bo nie tniemy kuli pionowo warunki na θ: 0 ≤ z ≤ 1 0 ≤ rcosθ ≤ 1

	1		π
0 ≤ θ ≤ arccos		, rmax = 2 ⇒ θ =
	r		3

	π
θ∊(0,		)
	3

	8
V = ∫02π dφ ∫0π3 dθ ∫02 r2cosθ dr = 2π ∫0π3		cosθ dθ
	3

	16		8√3
=		π [sinθ]0π3 =		π
	3		3

gacek: "warunki na θ: 0 ≤ z ≤ 1 0 ≤ rcosθ ≤ 1

	1
0 ≤ θ ≤ arccos		"
	r

Czy w 2 nierówności nie powinno być czasem:? 0 ≤ rsinθ ≤ 1 I skąd się wziął ten arcus?

Ada: Tak, arcsinus.

	1
sinθ =
	r

	1
θ = arcsin
	r

gacek: Okej, już chyba to rozumiem. Dzięki

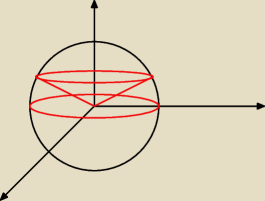
gacek: Hmm, jednak ten przykład nie daje mi spokoju. Skoro 'θ' zmienia się od zera do ^π₆ to dla tych warunków chyba wyjdzie taka bryła (ta co w treści zadania wraz z wciętym stożkiem).

gacek: ktoś jest w stanie napisać czy mam racje (jeśli tak to jak wtedy wyznaczyć obszary całkowania)?