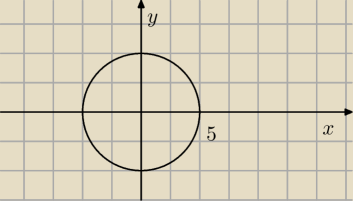
Zadanie z egzaminu Grzesiek: 4∫∫(x²+y²)e^[−(x²+y²)]dxdy D: x²+y²=25

Ada: x = rcosα y = rsinα x²+y² = r² r∊(0,5) α∊(0,2π) J = r I = 4 ∫₀^2π dα ∫₀⁵ r² e^−r2 r dr r² = t 2rdr = dt Całki są niezależne (jedna zależy tylko od kąta, druga tylko od promienia) można je więc liczyć niezależnie. ∫₀^2π dα = α]₀^2π = 2π

	1
I = 8π ∫025		t e−t dt = 4π ∫025 t e−t dt
	2

Całkując przez części: (pisane z pamięci polecam sprawdzić) I = 4π [−te^−t − e^−t ]₀²⁵ = ...

Karol: mam pytanie, skąd tam się wzięło r2 e−r2 r dr? dlaczego nie jest r2 e−r2 dr

Krzysiek: A czy rozwiązaniem tego nie jest 0? Mamy do czynienia z okręgiem a nie kołem...

Ada: Jeżeli nie jest to błąd w zapisie, to tak. Karol za x²+y² = r², e^−(x2+y2) = e^−r2 przemnażam to jeszcze przez Jakobian przejścia (bo zamieniam zmienne).