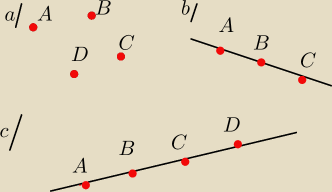
polprosta ,odcinek lamamna Powtórka: Czesc pierwsza zadania . dane sa uklady uklady punktow a) b) c) Biorac za poczatek polprostej ktorykolwiek z tych punktow i nprowadzac ja przez ktorykolwiek z innych wyznacz te polprosta . Ile takich roznych polprostych mozesz w ten sposob przeprowadzic wykorzystujac wszystkie punkty ukladu Wiec tak . rozpatrujac uklad a) z kazdego punktu mozemy wyprowadzic 3 polproste np z punktu A mozemy wyprowadzic polproste AB, AC AD . Wiec takich polprostych mozemy wyprowadzic 12 Uklad b wiec bedziemy mieli polproste AB i BC i chyba jeszce CB i BA wiec beda 4 polproste Uklad c) poplproste AB BC CD a takze DC CB BA wiec 6 takich polprostych Czesc druga zadania czy mozna tak dobrac uklad punktow aby wyznaczajac wszystkie mozliwe polproste jak w czesci pierwszej otrzymac nieparzysta liczbe poprostych (nie potrafie tego sobie wyobrazic )

Powtórka: Teraz tez wydaje mi sie ze w ukladzie b ) dojda jeszcze polproste AC i CA wiec bedzie 6 takich poprostych Natomiast w ukladzie c) oprocz wymienionych polprostych beda jeszce AC i CA BD i DB a takze AD i DA wiec wszystkich bedzie 12 polprostych Czyli tyle samo co w ukladzie a) czyli nie ma znaczenia czy punkty sa wspoliniowe czy niewspoliniowe . Prosze o odpowiedz i pomoc w czesci drugiej

Trivial: W podpunkcie b) nie da się rozróżnić półprostej AB od AC, gdyż C = B + α(B−A), gdzie α > 0. Nie wiem czy ta idea się sprawdzi, ale można pokombinować coś w tę stronę.

Powtórka: dziekuje bardzo Trivial jest to zadanie z 1 klasy liceum(poczatkowe ) wiec chyba bedzie prosciej Wobec tego w podpunkcie b ) beda tylko 4 polproste a nie 6 Tak samo a pdpunkcie c ) bedzie tylko 6 polprostych ?

Trivial: Tak. Odnośnie pytania drugiego, weźmy 4 różne punkty A,B,C,D. Rozważmy różne przypadki "posortowanych" trójek punktów: np. (A,B,C), (A,C,D), (A,B,D), ..., ale nie: (D,A,B), (D,B,A). a) W przypadku gdy żadna trójka punktów nie jest współliniowa, mamy 12 różnych półprostych. AB, AC, AD, BC, BD, CD BA, CA, DA, CB, DB, DC b) W przypadku, gdy dokładnie jedna trójka punktów jest współliniowa (załóżmy A,B,C − w tej kolejności na prostej) mamy 10 różnych półprostych AB, AC, AD, BC, BD, CD BA, CA, DA, CB, DB, DC c) W przypadku, gdy dokładnie wszystkie punkty leżą na jednej prostej, mamy 6 przypadków. AB, AC, AD, BC, BD, CD BA, CA, DA, CB, DB, DC Dowód formalny: Weźmy różne punkty: P₁, P₂, P₃, ..., P_n. Punkty te grupujemy we współliniowe "klastry": K₁, K₂, ..., K_m o rozmiarach 1 lub ≥3. Klaster K_s zawiera k_s punktów: k_s = |K_s| co daje warunek: k₁ + k₂ + ... + k_m = n. 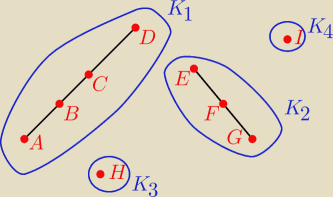Przykładowa klasteryzacja znajduje się na rysunku. Rozważmy ilość półprostych w różnych klastrach. a) Dla klastra o rozmiarze 1 możemy utworzyć 0 półprostych. b) Klaster o rozmiarze 2 nie jest zdefiniowany c) Klaster o rozmiarze 3 tworzy 4 półproste Klaster: A, B, C Różne półproste: AB, BC, CB, BA c) Klaster o rozmiarze 4 tworzy 6 półprostych Klaster: A, B, C, D Różne półproste: AB, BC, CD, DC, CB, BA d) Klaster o rozmiarze k tworzy 2(k−1) półprostych. Rozważmy ilość półprostych utworzonych między różnymi klastrami K_i, K_j. Jest ich 2k_ik_j, gdyż żadna trójka punktów z tych klastrów nie leży na jednej prostej. Wszystkich półprostych jest zatem: L = 2(k₁−1) + 2(k₂−1) + ... + 2(k_m−1) + 2k₁k₂ + 2k₁k₃ + ... + 2k₁k_m + 2k₂k₃ + 2k₂k₄ + ... + 2k₂k_m + ... + 2k_m−1k_m Suma liczb parzystych jest liczbą parzystą, zatem mamy dowiedzione.

Trivial: Eh. Jest błąd w dowodzie. Kto znajdzie niech też poprawi.

Powtórka: Moge tylko bardzo pieknie podziekowac za tak wyczerpujaca odpowiedz

Powtórka: Pewnie chodzi o to ze klaster o rozmiarze 2 jest zdefiniwalny (beda 2 polproste )

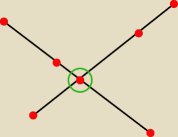
Trivial: W moim dowodzie brakuje rozważenia przypadku, kiedy jeden punkt jest współliniowy na kilka sposobów (patrz rysunek). Na razie nie mam na to pomysłu, ale czuję, że wystarczy drobna modyfikacja.

Trivial: A klaser o rozmiarze 2 nie jest zdefiniowany celowo − mamy wtedy 2 klastry o rozmiarze 1.

Powtórka: Dobrze . A powiedz mi czy to co teraz napisales to jest juz geometria wyzsza (czy znajde cos na ten temat np w ksiazce Podstawy geometrii Borsuk Szmielew ?

Trivial: "Geometrią wyższą" to bym tego nie nazwał. Po prostu spodobał mi się problem i spróbowałem go rozwiązać − sposób wymyśliłem sam. Gdzie można znaleźć informacje na ten temat niestety nie wiem.

Powtórka: Dobrze Bede tez pozniej probowal

Trivial: OK mam rozwiązanie. Wersja poprawiona: Weźmy różne punkty: P₁, P₂, P₃, ..., P_n. Punkty te grupujemy w maksymalne współliniowe "klastry" które mogą na siebie nachodzić: K₁, K₂, ..., K_m o rozmiarach 1 lub ≥3. Klaster K_s zawiera k_s punktów: k_s = |K_s| co daje warunek: k₁ + k₂ + ... + k_m ≥ n. Rozważmy ilość półprostych w różnych klastrach. a) Dla klastra o rozmiarze 1 możemy utworzyć 0 półprostych. b) Klaster o rozmiarze 2 nie jest zdefiniowany c) Klaster o rozmiarze 3 tworzy 4 półproste Klaster: A, B, C Różne półproste: AB, BC, CB, BA c) Klaster o rozmiarze 4 tworzy 6 półprostych Klaster: A, B, C, D Różne półproste: AB, BC, CD, DC, CB, BA d) Klaster o rozmiarze k tworzy 2(k−1) półprostych. NOWE: Rozważmy ilość półprostych utworzonych między różnymi klastrami K_i, K_j. a) Jeżeli klastry te nie mają części wspólnej, to można utworzyć 2k_ik_j półprostych. b) Jeżeli klastry mają jeden punkt wspólny, to można utworzyć 2(k_i−1)(k_j−1) półprostych. c) Nie ma innych możliwości Zdefiniujmy zatem liczbę a_i,j jako:

	⎧	kikj gdy Ki∩Kj = ∅
ai,j =	⎨
	⎩	(ki−1)(kj−1) gdy Ki∩Kj ≠ ∅

Wszystkich półprostych jest zatem: L = 2(k₁−1) + 2(k₂−1) + ... + 2(k_m−1) + 2a_1,2 + 2a_1,3 + ... + 2a_1,m + 2a_2,3 + 2a_2,4 + ... + 2a_2,m + ... + 2a_m−1,m Suma liczb parzystych jest liczbą parzystą, zatem mamy dowiedzione.

5-latek: Zaraz przepisuje do zeszytu

Trivial: Ciągle nie działa! Eh. mam dosyć.

5-latek: To nic nie szkodzi Moze jeszce dzisiaj albo moze jutro poprosze Mile o jakis pomysl na to

Maslanek: Brakuje chyba założenia, że każdy punkt może należeć do co najwyżej 2 klastrów, co? Albo rozważenie, co gdy punkt należy do więcej niż 3 klastrów?

5-latek: czyli jednak wyzsza geometria Nie dla ucznia klasy 1 liceum (technikum

Maslanek: Zawsze możesz szukać kontrprzykładu. Może by się udało Jeśli takie twierdzenie jak podaje Trivial nie jest prawdziwe

Maslanek: Już wiesz, że należałoby szukać, kiedy jeden punkt należy do 3 lub więcej klastrów jednocześnie. Więc musiałby należeć do trzech lub więcej prostych

5-latek: jesli Ci to nie przeszkadza to wrocmy do tego jutro wieczorem . Zaraz pora spac bo rano do pracy caly tydzien OK? Jutro tez wstawie inne zadania z tego paragrafu