pomocy ! asd: Przedstawić liczbę zespoloną w postaci trygonometrycznej: zo=1−i |z|=√1²+(−1)²=√2

	1
cosα=
	2

	−1
sinα=
	2

Nie wiem jak dalej doprowadzić do postaci trygonometrycznej, proszę o pomoc

Janek191: Źle policzone cos α i sin α

asd:

	1
sinα=
	√2

	−1
cosα=
	√2

Janek191:

	1		√2
cos α =		=
	√2		2

	−1		√2
sin α =		= −
	√2		2

	π
więc α = − 45o = −
	4

oraz

	π		π
z = I z I*( cos α + i sin α) = √2*( cos (−		) + i sin ( −		) ) =
	4		4

	π		π
= √2*( cos		− i sin		)
	4		4

===========================

Janek191: Teraz dobrze

asd:

	π
No tak tylko nie rozumiem co się dzieje z tym −		przy sin i cos, dlaczego minus wyłączamy
	4

	π		π
przed sin i dlaczego przy cos nagle z −		staje się
	4		4

Janek191:

Janek191: Bo cos ( − α) = cos α − funkcja parzysta oraz sin ( − α ) = − sin α − funkcja nieparzysta

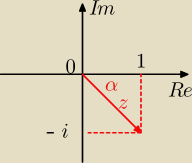
asd: Ok, dzięki ostatnie pytanko mam do Ciebie mam przykład, gdzie z=1−√3i

	1
cosα=
	2

	−√3
sinα=
	2

Jak w takim wypadku znaleźć α

unknown: − 60 stopni

asd: Czy będzie to tak wyglądało z=2(cos^π₃−sin^π₃}

asd: ?

asd:

	−π		π
Mam takie pytanko do tego dlaczego akurat wybieramy ujemny kąt czyli		a nie
	4		4

asd: up

Mila: 1) z=1−i |z|=√1²+1²=√2

	π		7π
φ=2π−		=
	4		4

	7π		√2
sin(		)=−
	4		2

	7π		√2
cos(		)=
	4		2

	7π		7π
z=√2*(cos(		)+i sin(		)
	4		4

2) z=1−√3i |z|=√1+3=2

	1
cosφ=
	2

	−√3
sinφ=
	2

	π		5π
φ=2π−		=
	3		3

Punkt(1,−√3) leży w IV ćwiartce

	5π		5π
z=2*(cos(		)+i sin(		))
	3		3