Twierdzenie sinusów Blue: Dany jest trójkąt ABC, w którym półprosta CP jest dwusieczną kąta ACB. Wykaż, że długości odcinków, na które dwusieczna dzieli bok AB, są proporcjonalne do długości boków AC i BC. Proszę o pomoc w tym zadaniu, wiem, że chyba trzeba tutaj wykorzystać twierdzenie sinusów, ale nie wiem, jak się za to zabrać

Ada: Nie trzeba wykorzystywać twierdzenia sinusów. Powstałe w ten sposób trójkąty mają jeden kąt otej samej mierze i jeden wspólny bok, więc są podobne

...: ... to trochę za mało jak na podobieństwo trójkątów−

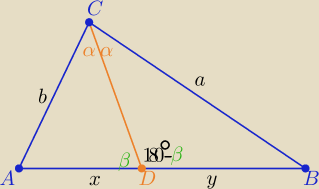
Eta: Z tw. sinusów w trójkątach:

	b		x		x		sinα
ADC :		=		⇒		=
	sinβ		sinα		b		sinβ

a

y

a

y

y

sinα

DBC:

=

=

=

⇒

=

sin(180o−β)

sinα

sinβ

sinα

a

sinβ

	x		y
to:		=		c.n.w
	b		a

Eta: Ada podała złą wskazówkę

Eta: Cechy podobieństwa trójkątów : (bbb) (bkb) (kkk)

...: ... dlatego Ją "skarciłem" ... pewnie pokalapućkało się Jej z prostokątnym −

Ada: Nie, dawno nie miałam geometrii i nie pamiętałam dokładnie jakie były warunki na przystawanie trójkątów, choć przed napisaniem tego powinnam sprawdzić, za czego nie zrobienie przepraszam. Hmm... choć w zasadzie twój post ... by lepiej o mnie świadczył

Blue: Eta Wielkie dzięki!